Автор: Ольга Леонтьева, 9360.g23@g23.relcom.ru
Дата публикации:01.11.2000
Соавторство: Константин Кноп
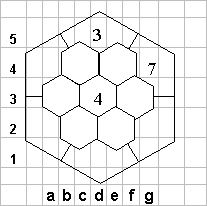
Эта головоломка возникла совсем недавно. Впервые она появилась на третьем очном чемпионате России по пазлспорту в июне 2000 года, и сразу понравилась многим. Суть ее очень проста: требуется расставить числа от 1 до 13 в соты, чтобы числа в соседних ячейках отличались хотя бы на 3. Обычно три числа уже стоят на своих местах. Но кажущаяся простота очень обманчива. Если пытаться решать головоломку "наугад", то можно напрасно потратить кучу сил и времени, так и не достигнув успеха. Неслучайно даже опытные головоломщики допускают ошибки, и во время проверки очень тяжело обнаружить cтоящие рядом, к примеру, шестерку и восьмерку, хоть известно, что правильно составленная задача всегда имеет единственное решение. Но как правило, в этих задачах существует логический, хоть и не совсем простой метод решения.

Рассмотрим решение головоломки, предлагавшейся на прошедшем 30 сентября 2000 года Чемпионате Украины. Во время соревнований с ней справились лишь около четверти участников. Будем обозначать соты также, как ранее обозначали клетки - с помощью цифры и буквы, хоть это менее удобно. Например, в данном условии в соте d3 стоит четверка, в соте d5 стоит тройка, а в соте g4 - семерка.
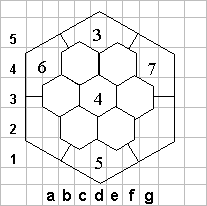
Вначале нужно исследовать возможное расположение цифр, близких к уже данным. Возникает естественный вопрос - где могут стоять цифры 5 и 6? Не рядом с четверкой, не рядом с семеркой, и не рядом друг с другом. Единственные возможные клетки для них - a4 и d1, при чем на а4 (рядом с тройкой) может стоять лишь шестерка. После этого рассуждения очевидного продолжения не видно, поэтому очень силен соблазн попытаться действовать наугад. Но не будем спешить это делать.
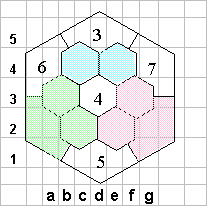
Лучше рассмотрим оставшиеся незаполненными восемь сот. Они естественным образом разбиваются на три группы, в каждой из которых все клетки касаются друг друга - голубую, розовую и зеленую. В одной группе не могут находиться числа, отличающиеся более, чем на 2. Поэтому, числа 8, 9 и 10, находятся в трех разных группах. Число 11 не может быть в одной группе ни с 10, не с 9, значит, только с 8. Аналогично, числа 9 и 12 находятся в одной группе, также как и числа 10 и 13 (но какая пара в какой группе - пока неизвестно). На первый взгляд, эти рассуждения не дают никакой новой информации. Но, продолжим исследования...
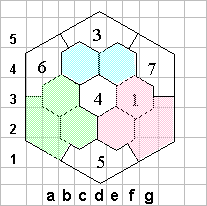
Рассмотрим соты е4 и f3, расположенные между четверкой и семеркой. Допустим, что оба числа в них больше семи. Тогда наименьшее из них -10, и подходит лишь пара 10-13. Но эта пара исключается, так как по нашим предыдущим рассуждениям, пара 10 - 13 должна быть в одной цветовой группе. Значит, в этой паре должна быть единица, причем стоящая не рядом с тройкой, а на f3.
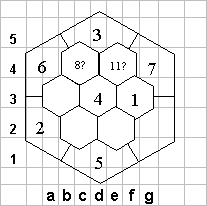
Теперь единственное возможное место для двойки - а2. Получилась цепочка из шести незаполненных сот: e 4 - c 4 - b 3 - c2 - e 2 - g2, в которые надо вставить числа от 8 до 13. Заметим, что числа 10 и 11 имеют лишь по одному возможному соседу (13 и 8 соответственно), поэтому должны стоять в концах этой цепочки (клетках e4 и g2). Если в е4 стоит 11, то в с4 (рядом с 6) должна стоять цифра 8 - нехорошо.
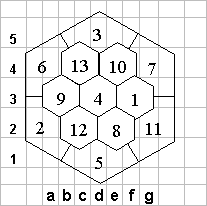
Поэтому в е4 стоит 10, а в g2 - 11. И оставшиеся клетки заполняются единственным возможным образом: в с4 - 13, в е2 - 8 , в с2 - 12, а в b3 - 9. Внимательно проверяем, что решение верно.