Автор: Ольга Леонтьева, 9360.g23@g23.relcom.ru
Дата публикации:18.09.2000
Соавторство: Константин Кноп
Головоломка "сапер" основана на широко известной игре "Minesweeper", имеющейся почти у всех обладателей MS Windows, начиная, кажется, еще с версии 2.0. Цель ее проста: исходя из данных ключевых чисел, восстановить расположение мин в прямоугольнике. Каждое ключевое число показывает, сколько соседних с ним клеток (из восьми) занято минами. Мины расположены по одной в каждой клетке, а в клетке с числом мин не бывает.
В головоломке, в отличие от игры, нельзя "щелкнуть" по клетке и в результате убедиться, что она пуста (или, наоборот, напороться на мину и затем начинать все сначала). Однако в головоломке гарантируется, что имеющейся информации (ключевых чисел) заведомо достаточно, чтобы однозначно отыскать все расположенные на поле мины. Здесь сапер может ошибаться более одного раза! Конечно, если все свои ошибки потом аккуратненько стереть карандашиком...
В некоторых вариациях предпочитают оперировать не с минами, а с алмазами на необитаемом острове. Суть головоломки от этого, разумеется, не меняется.
Иногда заранее оговаривается общее число мин, скрытых на данном поле. Эта информация может оказать существенную помощь в решении, а часто без нее решение перестает быть единственным.

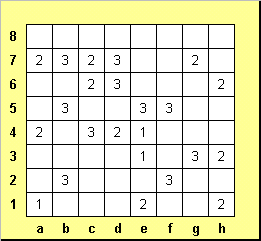
Рассмотрим процесс решения на примере небольшого квадрата. Общее количество мин в нашем случае неизвестно. Будем обозначать, как обычно, строки цифрами, а столбцы - буквами. Мины мы станем отмечать значками, а клетки, в которых мина находиться не может - зарисовывать голубым цветом. Процесс решения этой головоломки, как и многих других, складывается из отдельных рассуждений - мелких шагов. Все понимают, что если количество пустых клеток вокруг числа равно ему самому, то можно сразу заполнить все эти клетки минами. Но в профессионально сделанных "саперах" это редко встречается, как взятие фигуры на первом ходу в шахматной двухходовке. Поэтому первые шаги, как правило, должны быть более тонкими. Будьте внимательны!
Рассмотрим число 2 на клетке h3. Оно дает информацию, что в четырех клетках gh2 и gh4 расположены ровно две мины. Число 3 на g2 дает информацию, что в двух клетках f3 и f4 ровно одна мина (так как в остальных клетках, окружающих его - две мины). Отсюда можно сделать вывод, что остальные клетки, окружающие единицы на e3 и е4 - пусты. Закрашиваем их голубым цветом.
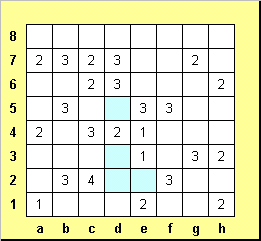
После этого две мины вокруг клетки d4 и три мины вокруг клетки е5 восстанавливаются однозначно.
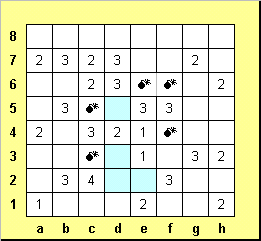
Остальные клетки вокруг f5 можно отметить, как пустые, что позволяет поставить однозначно две мины рядом с h6 - на h5 и h7.
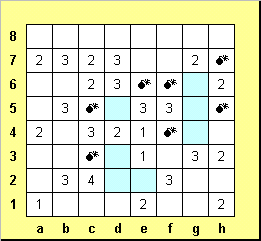
Каждый новый шаг тут же дает дополнительные возможности для осуществления новых шагов. Отмечаем пустые клетки вокруг g7, добавляем мину на е7 (чтобы вокруг d6 было ровно три мины). Отмечаем, что клетка f3 пуста, и как следствие - все оставшиеся клетки вокруг f2 заполнены минами.
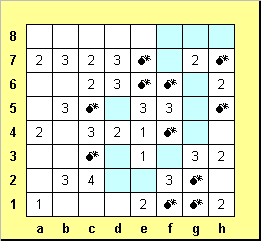
Отмечаем мину на d1 и на b6, красим голубым h2, затем ставим мину на h4.
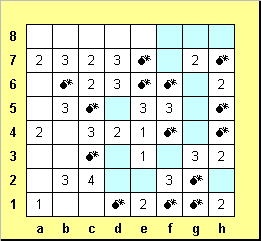
Когда кончились элементарные соображения, для продолжения решения необходимо снова использовать более тонкие рассуждения. Рядом с b7 ровно на одну мину больше, чем рядом с а7, эта мина может быть только на с8. Остальные клетки, соседние с с7, пусты, как и е8.
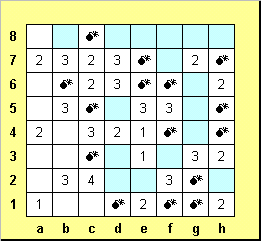
Цифра 4 на с2 означает, что в клетках b1, b3, и с1 имеется пара мин, которые вместе с миной на с3 полностью "обеспечивают" тройку на b2. Поэтому клетки а2 и а3 пусты. То есть мина для а1 находится в b1.
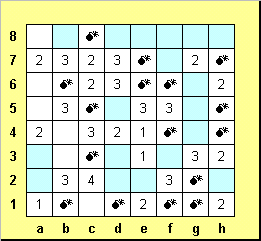
В клетках b3 и b4 ровно одна мина (за счет тройки в с4), поэтому мина есть в а5 (за счет двойки в а4).
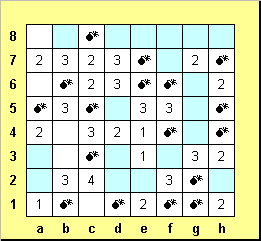
Осталось совсем немного - обозначить пустые клетки вокруг b5, мины в а8 и b3, пустую клетку с1. И обязательно убедиться, что в решении нет ошибок.
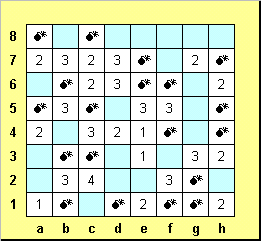
Вот и все! Ваша Ольга Леонтьева.