Автор: Ольга Леонтьева, 9360.g23@g23.relcom.ru
Дата публикации:18.12.2000
Об этой возникшей двенадцать лет назад головоломке можно рассказывать очень много и долго, тяжело ограничиться рамками нашего конкурса. Одно несомненно: различных изданий, посвященных ей, отечественных и зарубежных, куда больше, чем изданий, посвященных всем остальным головоломкам, вместе взятым. Головоломка уникальна во всём. И в том, что несколько человек оспаривают право на ее авторство. И в неимоверном количестве названий, вот лишь некоторые: нонограмма, рисование по числам (paint by numbers), японка. В России издатели решили добавить знакомое, раскрученное и коммерчески выгодное, хоть и не совсем уместное слово кроссворд, и теперь во всех киосках наряду со сканвордами можно увидеть сборники "японских кроссвордов". Но в нашем конкурсе место "японского рисования" (нам ближе именно это название) весьма скромно, оно лишь одно в ряду многих других.
Несомненный коммерческий успех японского
рисования вызван вовсе не головоломочной
уникальностью, а, скорее, психологическими
аспектами: человеку приятно как бы из ничего
получать некий готовый красивый продукт, в
данном случае - картинку. Если кто-то не знает, что
требуется, напомним: с помощью чисел закрасив
некоторые клетки, получить изображение. Числа
указывают длины связных закрашенных блоков в
соответствующей строке или столбце. Несмотря на
внешнюю красоту, японское рисование
предполагает лишь весьма ограниченный набор
рассуждений, помогающих продвинуться в решении.
И любой человек, посидев некоторое время, в
состоянии сам найти эти способы решения. Но все
же продемонстрируем процесс решения на
небольшом, но достаточно трудоемком примере.
Будем обозначать темно-зеленым закрашенные
клетки, а светлозеленым - пустые.
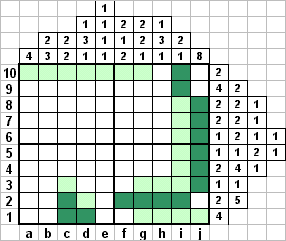
Вначале заполним очевидное. Если в линии стоит число, большее половины длмны линии, то несколько клеток в середине обязательно будут закрашены. Число 8 в столбце j позволяет закрасить клетки j3, j4, j5, j6, j7 и j8. Поскольку все правые числа в строках 3-8 равны 1, этот факт позволяет считать незакрашенными клетки i3, i4, i5, i6, i7, i8. Блоку длины 2 в строке i ничего не остается, как занять место i9 и i10. В строке 10 все левые семь клеток не закрашены, так как единственный блок длины 2 до них не дотянет.

В строке 2 рассматриваем самое левое и самое правое из возможных расположений блоков. Убеждаемся, что клетки f2, g2, и h2 всегда заняты блоком длины 5. Помечаем клетки g1, g3, h1, h3 как незакрашенные, ибо иначе не будет блока длины 1. Закрашиваем клетки с1 и d1, так как блок длины 4 в строке 1 их обязательно покроет, и помечаем как незакрашенные i1 и j1. Строим блок длины 2 в столбце с - закрашиваем с2 и помечаем незакрашенным с3. Помечаем как незакрашенную клетку d2. Закрашиваем клетку i1.
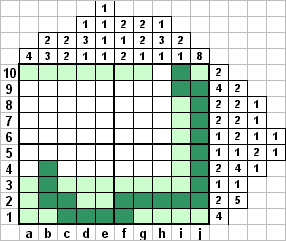
Отмечаем незакрашенным клетку а2 - блок длины 2 в строке 2 не дойдет до нее. После этого заодно оставляем незакрашенной и а1. Поэтому блок в строке 1 обязательно дойдет до е1, закрашиваем ее, а е2 отмечаем, как незакрашенную. Тут же окончательно устанавливаем положение блока длины 5 в строке 2, а затем - блока в столбце j. Полностью восстанавливаем и блок длины 2 в строке 2. И, исследуя возможное положение блока длины 3 в столбце b, закрашиваем b3. Все остальные клетки строки 3 помечаем, как незакрашенные. И, закрасив f1 (чтобы получился блок длины 2 в столбце f), полностью восстанавливаем строку 1. Теперь необходимо закрасить еще и b3.
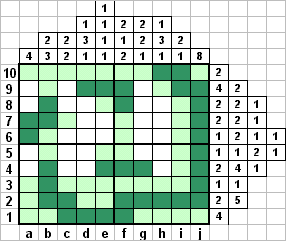
Закрашиваем h10 и отмечаем незакрашенным h9. Теперь определяем возможное положение блока в столбце а, закрашиваем а6 и а7. Расматриваем положение левого блока в строках 6 и 7, закрашиваем b7, помечаем как незакрашенные с7 и b6. Полностью восстанавливаем столбец b, закрасив блок длины 2, а оставшиеся клетки отметив незакрашенными. В строке 9 и строке 4 отмечаем клетки, которые наверняка будут заняты блоком длины 4. Полностью восстанавливаем столбец f, так как понятно, как там могут располагаться блоки. Помечаем незакрашенным клетки е8 и е5, чтобы в столбце е получились блоки длины 1.
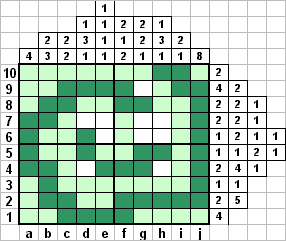
В строке 5 образовалось три пустых места для трех оставшихся блоков, поэтому однозначно вставляем блок длины 2 в клетки g2 и h2. Рассматривая столбец d, отмечаем незакрашенным d8; закрашиваем d5 и d6 - клетки, которые обязательно покроются блоком длины 3. Полностью восстанавливаем строку 5. Восстанавливаем столбец с, закрасив единственным возможным способом блок длины 2. Восстанавливаем однозначно строку 8. Наконец, в столбце а отмечаем единственное возможное положение блока длины 4.
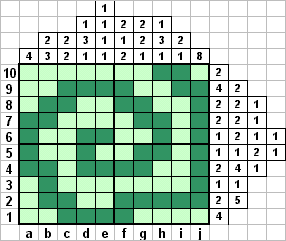
Отмечаем в строке 9 пустую клетку g9 и восстанавливаем столбец g. Осталось совсем немного. Можно закончить решение несколькими такими же логическими соображениями, как мы делали раньше. Но иногда имеет смысл продолжать или доканчивать решение, исходя из логики картинки. В нашем случае видно, что прорисовывается нечто, очень похожее на спираль. Так закончим это построение, проверив затем, не ошиблись ли мы. Все верно, мы не ошиблись. Задача решена. Процесс решения был совсем несложным, может быть, лишь немного громоздким.