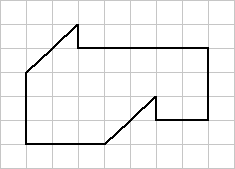
На рисунке слева - фигура, составленная из горизонтальных, вертикальных и диагональных отрезков. Задание состоит в том, чтобы разрезать ее одним разрезом на две равные (по размерам и форме) части.
Как правило, это можно сделать единственным образом. (Главное - догадаться, как). Ниже мы приведем некоторые полезные соображения.
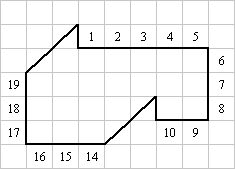
Соображение 1. Как бы ни проходила линия разреза, она делит границу (периметр) исходной фигуры на два равных по длине куска. Действительно, ведь периметр каждой из частей, на которые делится фигура благодаря проведенному разрезу, равен сумме длин разреза и границы исходной фигуры. Эти периметры равны, а разрез является общим для двух частей, поэтому и участки границы должны быть равными по длине.
Это соображение позволяет рассматривать тольк о те разрезы, концы которых являются "парными" друг другу - отстоят ровно на половину периметра границы. Например, если один конец разреза находится между цифрами 6 и 7, то другой должен быть между 17 и 18 (общий периметр фигуры на рисунке - 22).
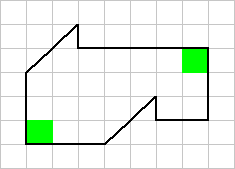
Соображение 2. Как правило, разрез не проходит через наиболее удаленные друг от друга углы фигуры.
Более того, если "расстояние по периметру" между какой-то парой углов равно половине периметра фигуры, то можно смело делать вывод, что эти углы соответствуют друг другу, то есть при совмещении двух разрезанных частей один угол должен наложиться на другой. На нашем рисунке такой парой углов являются две зеленых клетки.
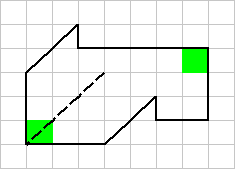
Теперь нужно понять, как именно должны совмещаться эти углы. Оказывается, есть всего два варианта того, как один угол "переходит" в другой: а) поворот на 180 градусов; б) этот же поворот + симметрия относительно штриховой линии.
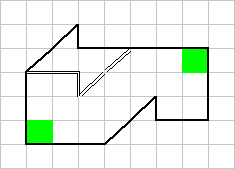
Вариант а). Линии проведены так, чтобы профиль разреза повторял профиль границы фигуры в правом нижнем углу. Очевидно, что такой разрез не годится: части получились неравными.
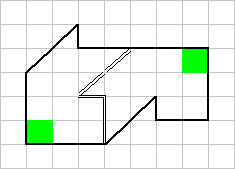
Вариант б). Проводим те же линии, но симметрично относительно диагонали (то есть снова ориентируемся по правому нижнему углу фигуры). Результат - то, что надо!
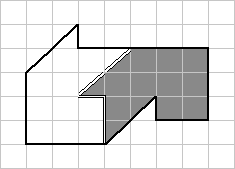
Вот, собственно, и все...