Как это мы делали и в других головоломках, обозначим столбцы буквами от a до f, а строки - цифрами от 1 до 6. Будем записывать найденные числа в клетки, желтым изображать клетки, в которых число находиться не может.
Вначале можно обратить внимание на следующие моменты.
- Если среди определяющих чисел есть пара одинаковых, то на пересечении соответствующих столбика и строки число находиться не может (иначе вторые числа в них совпадали бы).
- Если среди определяющих чисел есть простое число Р, то оно может быть представлено лишь как произведение Р и 1.
- Если среди определяющих чисел есть Р?, то оно может быть представлено лишь как произведение Р? и 1 (поскольку произведение Р и Р исключается).
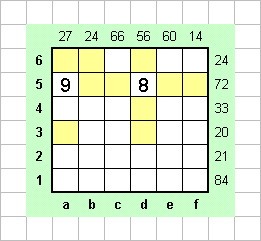
В нашем случае все эти рассуждения дают возможность лишь закрасить желтым клетку b6. Рассмотрим число 27 в столбце а. Оно может быть представлено лишь как произведение 3 и 9, поскольку ни одно из определяющих чисел строк не делится на 27. Но на 9 из этих чисел делится лишь 72, потому пишем 9 в клетке а5. Число 8 в строке 5 не может находиться в b5, так как тогда в обоих столбцах a и b присутствует число 3. Единственное оставшееся возможное место для него - в d5. Остальные клетки строки закрашиваем желтым, так же как и те клетки столбцов а и d, где числа 3 и 7 соответственно находиться не могут.
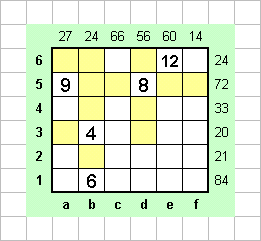
Число 24 может быть представлено как произведение многими способами: 24=1х24=2х12=3х8=4х6 Если рассматривать строку 6 и столбец b, то в них не может стоять ни уже использованное число 8, ни число 24, на которое не делится ни одно из других определяющих чисел. Поэтому в них могут быть лишь пары 2 - 12, и 4 - 6. Если пара 4 - 6 в строке 6, то 4 может стоять лишь в клетке е6, и получается противоречие с тем, что ни одно из определяющих чисел строк не делится на 15. Поэтому эта пара расположена в столбце b, единственным возможным способом, в клетках b3 и b6. А в строке 6 можно лишь определить точное положение числа 12: в клетке е6.
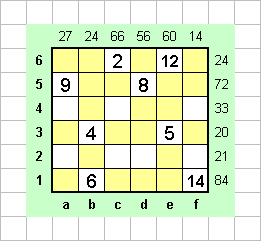
В клетку е3 прямо само просится число 5, остальные клетки столбца и сторки красим желтым, в строке 7 число 14 может находиться лишь в клетке f1, поэтому 2 не может стоять в f6, а только в с6.
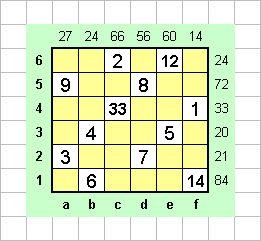
Осталось совсем немного: вписать 33 в единственно возможное место столбца с - в клетку c4, число 11 - в клетку f4, и закончить решение в строке 2, вписав оставшиеся числа 3 и 7 в клетки а2 и d2 соответственно.