Автор: Антон Никонов, antonick@mtu-net.ru
Дата публикации:04.11.2000
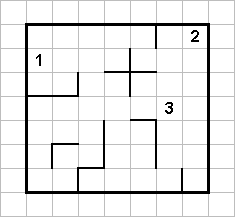
В этой головоломке требуется
расставить числа от 1 до N в табличку NxN
так, чтобы:
а) образовался магический квадрат, то есть сумма
чисел в каждой строке, каждом столбце и двух
диагоналях была одной и той же (а именно, 1+2+...+N).
б) для каждой линии, нарисованной внутри
таблички, сумма двух чисел, стоящих по разные
стороны от нее, равнялась N+1. И наоборот,
любую пару соседних чисел с суммой N+1 должна
разделять проведенная линия.
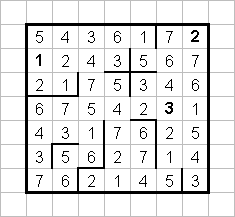
Мы расскажем о методике решения данного типа задач на примере квадрата 7х7. "Магическая сумма" для каждой пары цифр стоящих рядом с линией в данном случае равна 8. Кроме вертикальных и горизонтальных линий, в квадрате расположены три цифры. (Это минимально возможное количество заранее известных цифр для данной задачи.) Все остальные цифры можно расставить благодаря анализу расположения линий.
Посмотрим, как это сделать. Поскольку этот тип головоломок сравнительно нов, я, возможно, ещё не знаю всех приемов методики решения. Если кто-нибудь заметит что-либо интересное, прошу сообщить. С удовольствием готов обсудить.

Несложно определить, что сумма 8 может встретиться для трёх пар цифр: 1-7, 2-6, 3-5. Цифра "4" в этих суммах не испльзуется.
Действительно, если представить 8 как 4+4, то это будет означать, что две "четвёрки" стоят в одной строке или в одном столбце, что невозможно по условию задачи. Итак, ни одна из четвёрок не стоит рядом ни с какой из линий. Попробуем определить, где они могут располагаться. Проведём проверки для всех строк, столбцов и диагоналей.
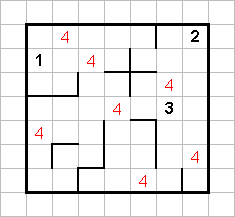
Результат обнадёживает: все четвёрки расставлены!
Посмотрим теперь на "крест", находящийся во второй и третьей строках. Какие цифры располагаются в прилегающих к нему 4 клетках? Очевидно, что это либо пары 2-6, 6-2, либо 3-5, 5-3. (Единица во второй строке уже стоит, значит, пары 1-7 здесь быть не может.)
Если попробовать расставить в "кресте" цифры 2-6, то нетрудно убедиться, что в этом случае на главную диагональ невозможно будет поставить двойку ни в каком месте.
Значит, в "кресте" могут быть только две пары 3-5, 5-3. Тогда двойки единственным способом ставятся во вторую и третью строки. А за ними и шестёрки.
Сделаем еще одно полезное наблюдение: поставил цифру - ищи куда поставить её "пару". Посмотрим на линии, на строки и на столбцы повнимательнее и расставим теперь все двойки и все шестерки:
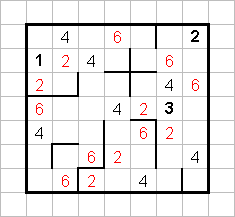
Вернёмся к "кресту". Он не позволяет паре 3-5 занять в шестой строке никакую другую позицию, кроме крайне левой, а в седьмой строке никакую другую, кроме крайне правой. Поставив пару 3-5 в седьмой строке, затем расставим все такие пары, не забывая и о диагоналях.
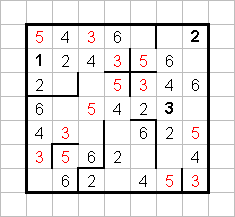
Во второй строке и в первом столбце таким образом образовались "вакантные места" для семёрок. Имеем право их расставить.
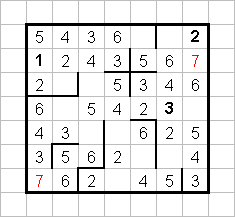
Ну а дальше-то уже и говорить не о чем. Сплошная механика. Задача решена! Спасибо за внимание.