Автор: Ольга Леонтьева, 9360.g23@g23.relcom.ru
Дата публикации:01.12.2000
Соавторство: Константин Кноп
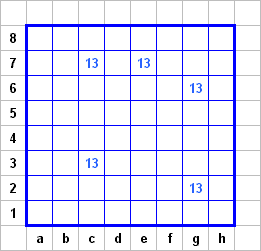
Эта головоломка американца Ника Бакстера (под названием "прямоугольные площади") была использована на прошедшем в октябре этого года чемпионате мира по пазлспорту. В ней требуется расположить несколько идущих по клеточкам прямоугольников, которые могут пересекаться, но не должны касаться друг друга, ни стороной или ее частью, ни даже углом. Каждое число означает сумму площадей всех прямоугольников, в которых оно находится. Особенность этой головоломки, в отличие от большинства встречающихся в нашем конкурсе - отсутствие строгих, стандартных алгоритмов при решении. То есть процесс восстановления прямоугольников не имеет готовых рецептов - его решатель должен увидеть, почувствовать сам, конечно, используя некоторые логические соображения. Разумеется, определяющие числа могут быть любыми, но поскольку на чемпионате использовалось лишь счастливое число, соответствующее номеру недели чемпионата, мы будем использовать этот факт в процессе решения.

Вот такой прямоугольник увидели участники в своих работах. Прежде чем начинать что-то чертить, немножко порассуждаем. Подумаем, как может число 13 быть представлено в виде суммы площадей двух прямоугольников (понятно, что больше двух прямоугольников быть не может). Разумеется, все вы самостоятельно сможете сделать перебор и убедиться, что возможные варианты - следующие: 1х13 (если одна из сторон прямоугольника не меньше 13), 3x4+1х1, 3х3+2х2, 2х5+1х3, 2х4+1х5, 3х3+1х4, 2х3+1х7.
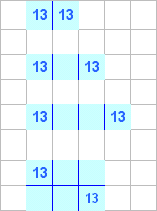
Отметим также еще вот какой факт: если два числа
стоят рядом, то они входят в один и тот же набор
прямоугольников. Действительно, если есть
прямоугольник, в который входит первое число, но
не входит второе, то должен быть и прямоугольник,
в который входит второе число, но не входит
первое, и эти два прямоугольника должны иметь
общий кусок стороны - между числами. Разумеется, в
общем случае, когда определяющие числа могут не
быть равными, это утверждение уже перестает быть
верным. Аналогично, числа через клетку или через
две должны иметь хотя бы один общий
прямоугольник. Также имеют общий прямоугольник
(причем - ровно один) числа, расположенные ходом
коня: граница любого прямоугольника, содержащего
ровно одно из этих чисел, имеет по крайней мере
две из выделенных семи сторон клеток. Разумеется,
если таблица достаточно большая, и возможно, что
число принадлежит лишь одному прямоугольнику
(1х13) утверждение перестает быть верным.
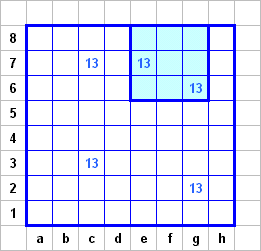
Вооружившись таким багажом, можно уже кое-что заметить в расположении чисел. Число на е7 должно иметь общий прямоугольник и с числом на с7, и с числом на g6. Второй из них не может быть ни 2х3, ни 2х4, ни 3х4 - только 3х3. Строим его таким образом (из двух вариантов), чтобы можно было еще построить пару прямоугольников площади 4, удовлетворяющих условиям задачи.
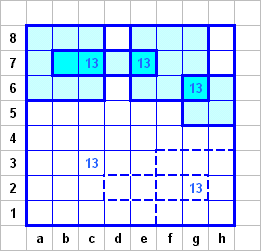
Строим единственным возможным образом эти прямоугольники - 1х4 и 2х2. Строим единственный возможный квадрат 3х3, необходимый для числа на с3. Подумаем, в какие прямоугольники может входить число на g2. Если это 3х3 и 1х4 (как на рисунке), то "испортится" число на с3. Оно испортится также, если использовать прямоугольники 2х3 и 1х7.

Убеждаемся, что единственный возможный вариант-
это прямоугольник 3х4, и внутри него - 1х1. И тут
начинается самое интересное - закончить решение
можно, оказывается, двумя различными способами:
построив еще один прямоугольник 3х4 с внутренним
квадратом 1х1,

или, как в авторском решении, прямоугольники 2х5
и 1х3. Вообще-то, традиционно считается, что паззлы
на чемпионатах должны иметь единственное
решение. Если решений несколько, то, конечно,
ничего фатального нет, они засчитываются всем
участникам, но это является некоторой
недоработкой составителей и усложняет работу
проверяющих.