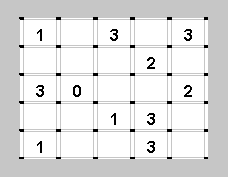
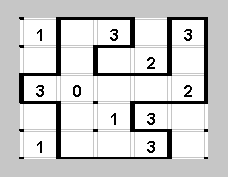
Условие задачи изображено на рисунке слева. Проведенные линии мы будем помечать черным цветом.
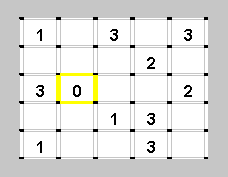
Те места, где линий быть не может, мы тоже будем выделять цветом - например, желтым. Для начала отметим желтым все границы вокруг клетки "0": ведь 0 по условию означает, что линий вокруг клетки нет.
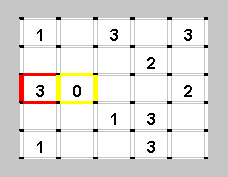
Теперь обратим внимание на цифру 3 рядом с нулем. "3" означает, что только по одной стороне (из четырех) не проходит линия. Поскольку эту сторону мы уже знаем, то около каждой из трех остальных сторон можем нарисовать линию (давайте договоримся свежепроведенные линии рисовать красным цветом, а на следующих рисунках изображать их уже черными).
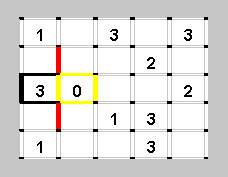
Подумаем, как можно продолжить уже нарисованные черные отрезочки. Очевидно, что один из них должен быть продлен вверх, а другой - вниз: других вариантов нет.
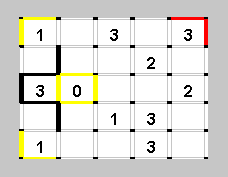
Теперь глянем в углы - это особый случай. Если ломаная проходит через угол, она должна пройти по обоим отрезочкам, примыкающим к нему. И наоборот, если ломаная не проходит через один из этих двух отрезков, то она не проходит и через другой. Поэтому в тех углах, где стоят единицы, можно смело рисовать два желтых отрезка, а в углу с цифрой 3, наоборот, рисуем два отрезка ломаной.
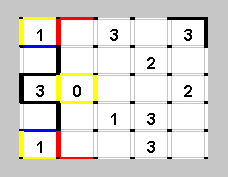
Что мы можем сказать о тех местах, которые выделены синим цветом? Линии через них проводить некуда! Поэтому около единиц, стоящих в левых углах, линии не слева, не сверху и не снизу, а справа (а потом заворачивают по горизонтали - см. рисунок слева)
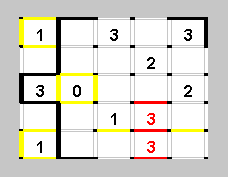
Внимание! Следующее используемое правило уже сложнее. Оно требует более подробного разбора и даже небольшого доказательства. (Проведите его самостоятельно.) В результате у вас должно получиться то, что изображено на этом рисунке: около двух соседних цифр 3 обязательно должны быть три горизонтальных отрезка - между цифрами, выше и ниже. А отрезки слева и справа от среднего можно смело красить желтым. (Почему?)
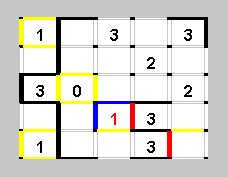
Рассмотрим синие границы вокруг красной цифры 1. Эти два отрезка сходятся в одном "узле" с двумя желтыми отрезками. Поэтому в этом узле ситуация аналогична той, которую мы видели в углу головоломки на шаге 3. Следовательно, и здесь на синих границах линии нет. Поэтому линия должна проходить справа от красной единицы. Кстати, после этого легко определяется и направление продолжения этой ломаной возле второй цифры 3.
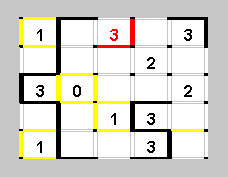
Теперь посмотрим на левый верхний угол возле красной тройки. Ломаная, пришедшая в него слева, затем должна обойти вокруг цифры 3. Это может быть сделано двумя способами - в результате непроведенной окажется либо линия на левой границе этой цифры, либо линия на верхней ее границе. В обоих случаях две других границы должны быть. Нарисуем там линии прямо сейчас!
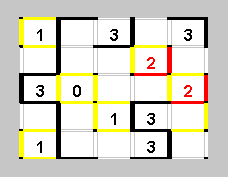
Пришел черед двух красных двоек. Сначала взглянем на верхнюю. Ломаная, огибающая цифру 3 выше и левее ее, не может "ветвиться" и проходить около нее. Поэтому выше и левее двойки границы желтые. Тогда ниже и правее мы вынуждены нарисовать два отрезка ломаной - больше им быть негде. Совершенно аналогично теперь можно разобраться и со следующей двойкой.
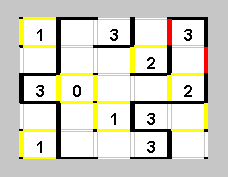
Правая вертикальная линия около нижней двойки должна быть продлена вверх - больше некуда. Но тогда она стыкуется с линией, которая огибает угловую тройку, и поэтому остается единственный вариант огибания угла - получается, что мы построили не одну, а сразу две вертикальных линии.
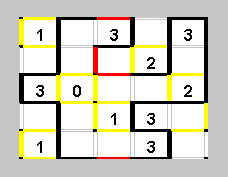
Осталось провести четыре красных отрезка, причем проводятся они единственным образом.
Ответ:
Не правда ли, все не так уж сложно?