КОМПЬЮТЕРРА
Как ускорить темп "жизни"?
Автор: Лев Наумов, lnaumov@chat.ru
Дата публикации:23.03.2001
Автор благодарит своих
учителей, особенно, учителя математики, Максима
Яковлевича Пратусевича, и учителя физики Сергея
Анатольевича Чивилихина, без которых ничего
этого бы не было. Отдельная благодарность Родиону
Горковенко
(Rodion.Gorkovenko@p14.f1194.n5030.z2.fidonet.org), который корректировал,
предлагаемую Вашему вниманию, статью и помогал
при разработке описываемых здесь идей.
Эффективная организация данных для
повышения скорости поиска клеток и разрешения
отношений соседства при реализации клеточного
автомата Джона Хортона Конвея “Жизнь”
Чтобы не обременять читателя, в
дальнейшем условимся называть этот автомат
просто игрой Жизнь. О правилах этой игры написано
немало, поэтому мы не будем останавливаться на
них, а сразу перейдём непосредственно к теме этой
статьи. Тем же, кто либо не знает правил, либо
просто хочет прочитать ещё раз о них, можем
порекомендовать книгу [1], с которой, пожалуй,
начинали все “жизнелюбы”, или книгу [4].
Идея применения вычислительных машин
для слежения за ходом игры – не нова. Сам Джон
Хортон Конвей использовал компьютер для
наблюдения за причудливыми конфигурациями
своего детища. Без моделирующих программ увидеть
большинство интереснейших превращений,
происходящих по ходу игры, было бы просто
невозможно. Некоторым вопросам написания таких
программ и посвящена данная статья.
 Итак, с точки зрения
программирования, Жизнь – трудоёмкая, для
компьютера, задача, так как требует довольно
больших ресурсов машины на непрерывный пересчёт
состояний моделируемого мира (под “миром”,
здесь и далее, будет пониматься плоскость,
разбитая на клетки, на которой рассматривается
колония). В чём же этот пересчёт заключается?
Фактически, на каждой итерации нужно разрешать
отношение соседства между конкретными
объектами, то есть, уметь узнавать, сколько у него
соседних клеток. Эта статья и посвящена именно
тому, как это сделать максимально эффективно
(ясно, что вариант полного перебора мест
гипотетической дислокации клеток мы
рассматривать не будем, тем более, что его
применение проблематично на “бесконечных”
полях, которые и представляют основной интерес
при моделировании процесса Жизни). Далее под
“местами” будем понимать позиции, на которых
могут стоять клетки, элементарную область в
рассматриваемом мире (“A” на
рисунке 1), а под “клетками” – места, в которых
есть жизнь (“B” на том же
рисунке).
Итак, с точки зрения
программирования, Жизнь – трудоёмкая, для
компьютера, задача, так как требует довольно
больших ресурсов машины на непрерывный пересчёт
состояний моделируемого мира (под “миром”,
здесь и далее, будет пониматься плоскость,
разбитая на клетки, на которой рассматривается
колония). В чём же этот пересчёт заключается?
Фактически, на каждой итерации нужно разрешать
отношение соседства между конкретными
объектами, то есть, уметь узнавать, сколько у него
соседних клеток. Эта статья и посвящена именно
тому, как это сделать максимально эффективно
(ясно, что вариант полного перебора мест
гипотетической дислокации клеток мы
рассматривать не будем, тем более, что его
применение проблематично на “бесконечных”
полях, которые и представляют основной интерес
при моделировании процесса Жизни). Далее под
“местами” будем понимать позиции, на которых
могут стоять клетки, элементарную область в
рассматриваемом мире (“A” на
рисунке 1), а под “клетками” – места, в которых
есть жизнь (“B” на том же
рисунке).
“Объектами” будем называть “клетки”
и “места”. Эту терминологию лучше запомнить, так
как она будет постоянно использоваться.
Конечно, приведённые здесь методы не
претендуют на то, чтобы быть истиной в высшей
инстанции, и автор с удовольствием будет
общаться с людьми, которые поделятся с ним своими
мыслями по этому поводу.
Любой мало-мальски серьёзный проект
начинается с продумывания и организации
структур данных, необходимых при решении задачи.
Первая дилемма, встающая перед нами – хотим мы
использовать динамические или статические
структуры для хранения информации о клетках. Под
статическими структурами имеется в виду,
конечно, массив. Очевидно, недостатков у этого
метода представления данных – более чем
достаточно. Хватит даже одного: размеры
популяции (число клеток в ней) неизбежно будут
ограничены. Зачем же он нужен? Метод, основанный
на использовании массива, программируется,
пожалуй, проще, чем любой другой. Иногда Жизнь
реализуют в декоративных целях: неплохая
экранная заставка – развитие случайно
сгенерированной популяции на поле, скажем, в 1024
на 768 мест, то есть, по пикселю на место. Зачем в
такой программе трудиться над списками или
другими динамическими структурами? Кроме того,
здесь – тривиальный способ ускорения разрешения
отношения соседства – сортировка.
1. Сортировка
Итак, пусть нам дан массив на
m элементов некоторой структуры, LifeCell, содержащей два информационных
поля. Допустим, такой структуры:
struct
LifeCell
{
int x,y;
};
 Будем хранить в
нём информацию о существующих клетках на данный
момент времени. То есть, если место с
координатами x0 и у0 является клеткой, то в массиве
должен присутствовать элемент, имеющий поля со
значениями x0 и y0. Пусть на данном шаге моделирования
у нас будет заполнено n
элементов. Так как размеры популяции, как
правило, не постоянны во времени, то n будет меняться от итерации к
итерации. Вот вам и очевидное ограничение: n не может превосходить m!
Будем хранить в
нём информацию о существующих клетках на данный
момент времени. То есть, если место с
координатами x0 и у0 является клеткой, то в массиве
должен присутствовать элемент, имеющий поля со
значениями x0 и y0. Пусть на данном шаге моделирования
у нас будет заполнено n
элементов. Так как размеры популяции, как
правило, не постоянны во времени, то n будет меняться от итерации к
итерации. Вот вам и очевидное ограничение: n не может превосходить m!
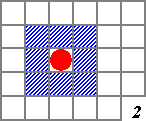
Как происходит разрешение отношения соседства
для объекта с координатами
x0, y0? Для него нам нужно найти в массиве
все соседние клетки (смотрите рисунок 2), тогда
остальные его соседи являются местами. Обращаем
Ваше внимание на то, что такой поиск нужно
производить не только для n
клеток, которые содержатся в массиве, но и для
всех окружающих их объектов, то есть именно, для
ближайших восьми соседей, так как это – места
гипотетического возникновения жизни. Таким
образом, на каждой итерации придётся разрешать
отношение соседства для 9*n
объектов (n клеток, у каждой –
8 соседей).
Как сделать это максимально
эффективно? Конечно, отсортировав массив по
возрастанию (или по убыванию) одной из координат,
скажем, по y. Тогда будет
достаточно только пробежать в массиве интервал
ячеек, для которых значения y-координат
элементов будут заключены между y0-2 и y0+2.
Остальные клетки рассматривать уже
бессмысленно, так как они слишком далеки от
нашего объекта. Затем нужно перейти к следующему
объекту или следующей ячейке массива. Разрешать
отношения соседства в строгом порядке,
установленном расположением ячеек в массиве –
очень рационально. Поступаем так: рассмотрели
соседей клетки, содержащейся в ячейке массива с
номером i, рассмотрели
соседей её соседей – перешли к следующей (к (i+1)-ой). Тогда счётчик (индекс)
обрабатываемой ячейки i
поможет нам рассмотреть весь вышеописанный
интервал и будет достаточно просто “пройтись”
от i-ой ячейки вправо и влево
по массиву до тех пор, пока y-координаты
клеток не будет отличаться от y-координаты рассматриваемого
объекта на два.
Здесь, вообще говоря, нужно
организовать просмотр так, чтобы не приходилось
по несколько раз учитывать одни и те же клетки,
ведь любая из них – соседка своего соседа, но в
рамках этой статьи методы преодоления этой
проблемы мы рассматривать не будем, так как она
имеет лишь косвенное отношение к
непосредственной тематике статьи.
После того, как с соседями станет всё
ясно, вносим в массив необходимые изменения, и,
перед переходом на следующую итерацию, лишь
сортируем его. Для этого можно использовать,
например, алгоритм QuickSort,
предложенный в 1962 году английским математиком
Чарльзом Хоаром (его ещё можно встретить под
названием “быстрая сортировка”). Для его
изучения, можем порекомендовать книгу [2], где
есть много интересной информации об алгоритмах
сортировки вообще (на самом деле – и не только
сортировки, а практически всех базовых
алгоритмов, в том числе и упоминаемых далее в
этой статье) и QuickSort, в
частности.
Опыт показывает, что сортировка внутри
групп с одинаковыми y-координатами
по x-координатам даст
ощутимый эффект лишь при достаточно больших
размерах популяции. Тем не менее, иногда, это всё
же имеет смысл и тогда по x-координатам
стоит проводить поиск дихотомией (“двоичным
поиском”). Описание этого алгоритма, как, кстати,
и алгоритма QuickSort, можно
найти, например, в книге [3].
От статических структур переходим к
динамическим. Как Вы понимаете, сортировать
список – не лучшая идея. Несмотря на то, что
существует множество алгоритмов для этого, но
сочетать динамические структуры, с тем же
методом, который мы использовали для статических
– не разумно, так как его реализация будет
намного более сложной. Однако, справедливости
ради, необходимо отметить, что трудоёмкость
“ленточной сортировки” (метода упорядочивания
списков) такая же, как и у QuickSort’а,
то есть O(N*ln(N)), где N – число сортируемых элементов. Но к
динамическим структурам применимо такое
мощнейшее средство, как хеширование.
2. Стандартные принципы хеширования и
их применение к Жизни
Хеширование (от английского “hash” – “размешивать”) служит для
оптимизации задач обработки информации, а
конкретнее, преимущественно, для интересующего
нас поиска (для нас важна именно эта операция,
ведь как бы мы не организовали хранение
информации, по всему её объёму, придётся искать
соседей некоторого объекта).
Метод хеширования позволяет
производить это более эффективно. Его принцип
заключается в разбиении всего набора данных на
маленькие группы, с которыми быстрее
оперировать. Для этого информационным полям
конкретной структуры, сопоставляется значение
некой функции. Так называемой, хеш-функции.
Разбиение на группы, “размешивание” информации,
происходит по признаку равенства этого значения
(оно ещё называется ключом). Нужно стремиться к
тому, чтобы группы были приблизительно
одинаковыми по величине. Когда мы знаем
содержимое полей структуры, которую хотим найти
и можем произвести подсчёт ключа для неё, то
после этого, искать точное совпадение требуемых
полей нужно уже не по всему набору данных, а лишь
в рамках группы, отвечающей конкретному
полученному значению хеш-функции. В худшем
случае, хеширование приведёт к обычному поиску
полным перебором (справедливости ради надо
отметить, что так будет лишь с точки зрения
трудоёмкости, на практике получится ещё
медленнее из-за “холостого прокручивания”
механизма хеширования). Но для этого нужна
поразительно неудачная хеш-функция, выдающая
одинаковые значения ключа для всех
объектов-структур, содержащихся в наборе данных,
по которому производится поиск. Подробности об
этом методе можно найти в, уже упоминавшейся в
этой статье, книге [2].
Достаточно эффективный способ
применения такого метода – организация массива
указателей на списки. Каждый из этих списков
содержит структуры, значения хеш-функции для
которых одинаково (это – вышеописанные группы), а
индекс ячейки массива, содержащей указатель на
данный список, равен её значению (этот способ
будет широко использоваться в следующих
параграфах). Также, вполне благоприятен вариант,
когда индекс равен некоей функции от её значения.
Ведь, например, в языках C/C++
массивы индексируются от нуля, и если наша
хеш-функция принимает целые значения от 7, то
функция преобразования индекса должна будет
вычитать из получающегося ключа семёрку.
Впрочем, эту функцию преобразования, в таком
случае, имеет смысл включить в процедуры
подсчёта хеш-функции.
Итак, возвращаясь к нашему примеру,
продолжим рассмотрение данных, хранящихся в
объектах вышеописанного типа LifeCell. Теперь, когда нам понадобится
посмотреть, является ли клеткой место (x0+1;y0-1), мы сосчитаем хеш-функцию от
данных значений полей, а потом поищем информацию
о ней не среди всех клеток, а среди лишь членов
списка, для которых она имеет то же значение.
Хеширование особенно эффективно для больших
колоний, когда выигрыш от его применения окупает
накладные расходы на его реализацию, а число
клеток на порядок больше числа возможных
значений ключа.
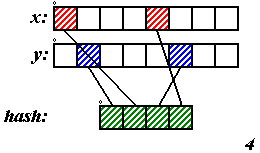
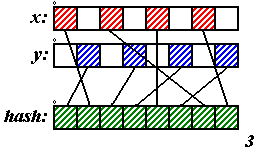
Очень часто в качестве хеш-функций
применяются битовые операции. Пусть x, y и ключ занимают по одному байту,
тогда последний можно по битам составить так, как
показано на рисунке 3. Если целого байта под ключ
жалко, то можно использовать четыре бита, как
предложено на рисунке 4 (для обоих рисунков будем
считать, что младший бит – слева). Конечно,
эффективность этого метода зависит от набора
данных, на котором он используется. Скажем, точки
(255;0), (150;45), (166;37), (200;139) размешаются хеш-функцией,
изображённой на рисунке 3 хорошо, все – в разные
списки, а точки (85;239), (117;238), (87;171), (213;170) – все в
один.
На самом деле, нет никаких
принципиальных ограничений на используемые
хеш-функции, кроме границ здравого смысла. Помимо
побитовых преобразований, это могут быть просто
математические функций или композиции тех и
других. Но не надо слишком мудрствовать.
Надеемся, например, синус суммы x и y вряд ли
кто-нибудь будет использовать в качестве
хеш-функции, по крайней мере, применительно к
Жизни.
Ключ должен быть достаточно короток,
чтобы расходы на него были позволительны и в то
же время, достаточно длинен, чтобы хорошо
“размешивать” данные (чем больше мощность
множества значений ключа, тем больше разных
групп можно составить, тем меньше в них будет
элементов (но хотелось бы, чтобы они всё же были в
каждой группе и, чтобы их количество для всех
групп было почти одинаковым или хотя бы одного
порядка) и тем быстрее по ним будет производиться
поиск).
Изображённые на рисунках 3 и 4 модели
получения ключа по полям
LifeCell
используют некие общие соображения теории
хеш-функций, абстрагируясь от специфики задачи.
Как было указано выше, есть наборы клеток,
которые эти функции размешают крайне плохо.
Давайте всё-таки вспомним, что мы моделируем
именно Жизнь.
3. Более “Жизненное” хеширование
Зададимся двумя целыми параметрами
a и b и матрицей
указателей на списки mat
(далее, говоря “хеш-таблица”, будем иметь в виду
именно её) размера a на b. В качестве ключей хеширования
(здесь их будет даже два) предлагается
использовать остатки от деления x на a в первом
случае и y на b, во втором. Вот примеры реализации
таких хеш-функций для x и для y, соответственно:
int
HashX(int x)
{
return
x%a;
}
int
HashY(int y)
{
return
y%b;
}
Очевидно, что результатом выполнения
первой функции будет целое число из отрезка от 0
до a-1, а второй – от 0 до b-1. Пусть, после одного
такого вычисления мы получили f – как значения
ключа для x, а g – для y некоторой точки (x0,y0).
Тогда мы должны будем искать информацию о том,
является ли место (x0,y0) клеткой в
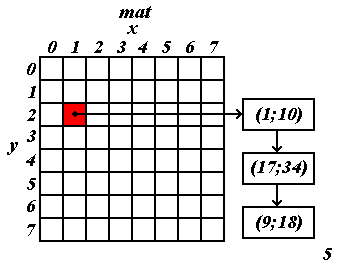
списке, на который указывает mat[f,g]. На рисунке 5
приведён пример такого размещения, в котором
положено a=8 и b=8, хотя, вообще говоря, a и b вполне
могут быть (а скорее, даже, должны быть) не равны,
что мы будем наблюдать в дальнейшем.
Так в чём же обещанное преимущество
хеш-метода, описанного в этом параграфе, над
общим, описанном в предыдущем? Дело в том, что
этот метод – адаптивный, то есть он может
повышать свою эффективность, в зависимости от
конкретных данных, “переразмешивать” структуры
вследствие анализа своей собственной работы.
4. Адаптивное хеширование
Как Вы уже, наверное, догадались,
механизм “переразмешивания” основан на
изменении
a и b. Когда списки, “прицепленные” к
разным ячейкам матрицы, слишком сильно
отличаются по размеру, следует изменить
параметры хеширования (a и b) и, как следствие, размеры нашей
таблицы. Вернёмся снова к случаю, когда оба
параметра равны восьми, рассмотренному нами в
предыдущем параграфе. Клетки с координатами 1, 9,
17, … , и вообще, вида 1+8k (где k – некое целое число), в таком случае,
попадут в один список (ещё раз взгляните на
рисунок 5). Как нужно поменять a
и b, чтобы исправить ситуацию?
Посмотрите на таблицу №1.
Таблица №1 |
Делитель |
Делимое |
1 |
9 |
17 |
25 |
33 |
41 |
49 |
57 |
65 |
73 |
81 |
89 |
97 |
105 |
113 |
121 |
129 |
137 |
145 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
1 |
4 |
2 |
0 |
3 |
1 |
4 |
2 |
0 |
3 |
1 |
4 |
2 |
0 |
3 |
1 |
4 |
2 |
0 |
6 |
1 |
3 |
5 |
1 |
3 |
5 |
1 |
3 |
5 |
1 |
3 |
5 |
1 |
3 |
5 |
1 |
3 |
5 |
1 |
7 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
1 |
0 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
10 |
1 |
9 |
7 |
5 |
3 |
1 |
9 |
7 |
5 |
3 |
1 |
9 |
7 |
5 |
3 |
1 |
9 |
7 |
5 |
11 |
1 |
9 |
6 |
3 |
0 |
8 |
5 |
2 |
10 |
7 |
4 |
1 |
9 |
6 |
3 |
0 |
8 |
5 |
2 |
12 |
1 |
9 |
5 |
1 |
9 |
5 |
1 |
9 |
5 |
1 |
9 |
5 |
1 |
9 |
5 |
1 |
9 |
5 |
1 |
13 |
1 |
9 |
4 |
12 |
7 |
2 |
10 |
5 |
0 |
8 |
3 |
11 |
6 |
1 |
9 |
4 |
12 |
7 |
2 |
14 |
1 |
9 |
3 |
11 |
5 |
13 |
7 |
1 |
9 |
3 |
11 |
5 |
13 |
7 |
1 |
9 |
3 |
11 |
5 |
15 |
1 |
9 |
2 |
10 |
3 |
11 |
4 |
12 |
5 |
13 |
6 |
14 |
7 |
0 |
8 |
1 |
9 |
2 |
10 |
16 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
17 |
1 |
9 |
0 |
8 |
16 |
7 |
15 |
6 |
14 |
5 |
13 |
4 |
12 |
3 |
11 |
2 |
10 |
1 |
9 |
18 |
1 |
9 |
17 |
7 |
15 |
5 |
13 |
3 |
11 |
1 |
9 |
17 |
7 |
15 |
5 |
13 |
3 |
11 |
1 |
19 |
1 |
9 |
17 |
6 |
14 |
3 |
11 |
0 |
8 |
16 |
5 |
13 |
2 |
10 |
18 |
7 |
15 |
4 |
12 |
20 |
1 |
9 |
17 |
5 |
13 |
1 |
9 |
17 |
5 |
13 |
1 |
9 |
17 |
5 |
13 |
1 |
9 |
17 |
5 |
21 |
1 |
9 |
17 |
4 |
12 |
20 |
7 |
15 |
2 |
10 |
18 |
5 |
13 |
0 |
8 |
16 |
3 |
11 |
19 |
22 |
1 |
9 |
17 |
3 |
11 |
19 |
5 |
13 |
21 |
7 |
15 |
1 |
9 |
17 |
3 |
11 |
19 |
5 |
13 |
23 |
1 |
9 |
17 |
2 |
10 |
18 |
3 |
11 |
19 |
4 |
12 |
20 |
5 |
13 |
21 |
6 |
14 |
22 |
7 |
24 |
1 |
9 |
17 |
1 |
9 |
17 |
1 |
9 |
17 |
1 |
9 |
17 |
1 |
9 |
17 |
1 |
9 |
17 |
1 |
Здесь приведены остатки от деления
чисел указанного вида на целые числа от одного до
двадцати четырех. Жёлтые строки не представляют
для нас никакого интереса, так как изменение
параметра хеширования на соответствующие им
значения делителя не приведут к
“переразмешиванию”, а сохранят текущую
группировку информации, то есть, всё, что было в
одном списке – в одном же и останется. Только
количество списков уменьшится, вследствие их
объединения прямо целыми группами (например, это
произойдёт, если поменять значение
a с 8 на 4). Остальные строки разделены
на розовые и голубые зоны. Эти зоны представляют
собой периоды значений хеш-функции (два соседних
периода выделены разными цветами, для
наглядности) если параметр размешивания принять
равным соответствующему делителю. В рамках
рассматриваемой нами задачи, ясно, что все
значения хеш-функции внутри одного периода не
повторяются, тогда длина периода и есть
количество списков, на которые разобьётся
группа, имеющая непомерно большое, в нашем
понимании, число элементов. Если мы
рассматриваем в данный момент хеширование по x-координате, а d –
делитель, претендующий на то, чтобы стать
параметром размешивания (для определённости – a), то это длина (обозначим её, как len), очевидно, равна max(a,d)/nod(a,d), где функция max
возвращает максимум двух чисел, а nod – их наибольший общий делитель.
Теперь мы можем просто сформулировать, что для
жёлтых строк len=1.
Какое же
d принять
за новое значение a? Конечно,
лучше – то, которому соответствует наибольшая len. Тогда, одним из критериев
оптимального решения является то, чтобы nod(a,d)=1 или, проще говоря, чтобы a и d были взаимно
простыми. Ясно, что можно найти сколь угодно
большое d, удовлетворяющее
этому условию. Вообще предел len, при d
стремящемся к бесконечности, равен
бесконечности, но с практической точки зрения
нам бы не очень хотелось непомерно расширять mat. Поэтому “лучше, чтобы nod(a,d) равнялся единице”, так как тогда
меньшим d будет
соответствовать большая len.
Так всё-таки, в каких пределах лучше
искать
d? Наверное, самым
правильным будет завести неких базовый уровень t, в окрестности которого найти d1 и d2, такие, что d1<a, а d2>a и оба
“достаточно хорошо” переразмешают клетки.
Потом выбрать из них то, которое ближе к t. Что значит “достаточно хорошо
перемешивает”? Как уже не раз говорилось, это
значит так, чтобы все группы были приблизительно
равных размеров. Методы повышения эффективности
установления этого мы можем обсудить.
Нужно отметить, что t может меняться от итерации к
итерации. Можно использовать в качестве t кубический корень из числа клеток
на данном шаге (округлённый, естественно), тем
более что число клеток, как правило, является
важным параметром работы клеточного автомата и
почти всегда вычисляется и отображается на
экране. Однако, при использовании этого метода
бывает эффективным пересчитывать t не каждый раз, а через один или два
раза, в зависимости от периодичности колонии,
развивающейся в конкретном мире (это – очень
интересная тема, может кто-то хочет что-нибудь сказать или спросить по этому поводу).
Что такое, эти пресловутые, группы
“приблизительно равных размеров”? Как понять,
что построенная хеш-таблица требует
“перетряхивания”? Предлагается следующий
метод: при каждом её изменении, обусловленном
событиями, происходящими с колонией, считать
среднее арифметическое числа элементов в списке.
Здесь можно воспользоваться тривиальным
свойством среднего арифметического: если нам
известно его значение An
для n чисел, то, если добавить
к набору чисел, для которого производится
вычисление, ещё одно число q,
то для n+1 числа An+1=(nAn+q)/(n+1). Например, можно написать это
как-то так:
void
AddValue(int q, float& A, int& n) // Функция, осуществляющая
добавление к набору n чисел, по которому
считалось среднее арифметическое A, числа q
{
A=(A*n+q)/(++n);
}
void
Iteration()
{
float A=0; // Текущее
значение среднего арифметического
int n=0; // Текущее
количество значений. В терминах
вышеприведённого текста, для данного n A
представляет собой An
int q=0; //
Добавляемое значение
<Код программы, в котором, в
частности, как-то задаётся q>
AddValue(q, A, n);
//
Непосредственно добавление значения. Как
правило, оно происходит в некотором цикле
<Код программы>
}
Пусть результат подсчёта среднего
помещён в
A. Так, если
изначально задать некое целое положительное
число r, то перестраивать
хеш-таблицу следует, если число клеток в
некотором списке в r раз
больше, чем A. Для быстрейшей
проверки этого соотношения имеет смысл
представить mat не как матрицу
указателей, а, например, как матрицу записей с
двумя полями: одно из которых – указателей, а
второе – длина списка, на который он указывает.
Подсчитав сумму этих длин, можно заодно выяснить
и число клеток на данном шаге, что может быть
полезно (смотрите несколько абзацев выше) или
намного более простым способом подсчитать A. Зачем же тогда нужен описанный выше
способ определения среднего? Дело в том, что есть
ещё один вариант, экономящий память, но теряющий
в эффективности. Можно сравнивать r, умноженное на A,
со значениями длин списков, полученными на
следующей итерации (их всё равно нужно считать
для следующего значения среднего
арифметического). Таким образом, A, “отстаёт” на один шаг. Почему это
вообще имеет смысл? Ответ лежит только в узко
специфических особенностях Жизни по правилам
Конвея (2 соседа, чтобы не умереть, 3, чтобы
родиться) или близких к ним, но никак не что-то
вроде 1, 6 и 7, чтобы умереть и 2, 3 и 5, чтобы родиться,
Жизнь по которым даже представить трудно.
Во-первых, это обусловлено периодичностью
стационарных состояний, а во-вторых, тем, что
“сфера влияния” клетки – её ближайшие соседи и
за один шаг она не может “переместиться” дальше,
чем на одно место. Таким образом, стоящая в
списке, на который указывал mat[u,v] клетка, не попадёт никуда, кроме,
как в один из восьми списков: mat[u,v+1], mat[u,v-1],
mat[u+1,v+1], mat[u+1,v], mat[u+1,v-1], mat[u-1,v+1], mat[u-1,v] или mat[u-1,v-1].
Думаете, игра не стоит свеч? Напрасно! Попробуйте.
Конечно, намного эффективнее (или, по крайней
мере, логичнее) рассматривать A с текущими значениями длин списков,
но как промежуточный вариант это очень не плохо.
А если Вы программируете Жизнь под DOS’ом, то это – просто способ
сэкономить память ещё на несколько сотен клеток.
Кроме того, это можно рассматривать просто, как
расширение описываемого метода хеширования,
вносящее дополнительную неопределённость в
результат.
Константу
r
выбирайте также осторожно, чтобы слишком частые
“перестройки” не затормаживали работу машины
из-за большой трудоёмкости, а слишком редкие –
из-за неэффективного поиска.
Не стоит применять методы определения
необходимости перестройки
mat,
основанные на разности минимальной и
максимальной длин списков. Почти всегда минимум
будет равен нулю. Вообще, лучше избегать
абсолютных отклонений при хешировании, намного
практичнее использовать относительные.
Наверное, у Вас возникает абсолютно
справедливый вопрос: а какие
a
и b использовать при первом
шаге программы? Да хоть уже не раз упоминавшиеся
значения 8! А лучше – a=8, а b=7, чтобы первая же итерация с
диагонально-растянутыми колониями не
потребовала переразмешивания. Однако, метод
адоптивный и mat всё равно
будет перестраиваться под конкретную ситуацию
на поле. Лучше выбирайте их не очень большими,
помните, раз в итерацию Вам придётся пробегать
матрицу размером a на b, делая, прямо скажем, не тривиальные
операции. Поэтому и было упомянуто, что можно
использовать t, как плавающую
границу. Пример такого метода: задаться
некоторым параметром w и
считать t, не, как было
предложено выше, как кубический корень из числа
клеток, а как корень степени w,
чтобы, варьируя w от 3 до
“бесконечности”, удерживать t в разумных для используемого
компьютера пределах. То есть так, чтобы пересчёт
занимал время, не обременяющее пользователя.
Однако, нужно иметь в виду, что чем больше a и b, тем быстрее,
для хорошо размешанных данных, осуществляется
поиск клетки.
Здесь приведён далеко не полных список
возможных методов эффективной организации
данных при программировании такой интереснейшей
игры, как Жизнь. Кроме того, они немного
адаптированы под статью. Ведь на практике, вместо
массива структур с двумя полями, очевидно, лучше
применять просто два массива. Однако, информация,
представленная в этой статье, пожалуй, может
послужить хорошей отправной точкой или, по
крайней мере, поводом для размышлений. Автор с
удовольствием будет общаться с теми,
кто имеет, что сказать по данному
вопросу или вообще, поводу алгоритмов реализации
Жизни, форматов файлов, хеш-функций, логики
построения, математики, или с теми, кто просто
хочет пообщаться на тему клеточных автоматов в
целом и Жизни, в частности. Может быть, кто-то
реализовывал что-то подобное на практике или
воспользовался вышеописанными советами при
написании программ? Вообще, поделитесь,
пожалуйста, впечатлениями о статье.
Литература:
- Гарднер М.
Математические досуги. – М.: Мир, 1972,
страницы 458-488;
- Ахромеева Т.С., Дородницын В.А., Еленин Г.Г.,
Курдюмов С.П., Малинецкий Г.Г., Потапов А.Б.,
Самарский А.А.
Компьютеры и нелинейные явления:
Информатика и современное естествознание / Под
редакцией Самарского А.А. – М.: Наука, 1988, страницы
5-43;
- Кормен Т., Лейзерсон Ч., Ривест Р.
Алгоритмы:
построения и анализ. – М.: МЦНМО, 2000, страницы 135-180,
213-236;
- Романовский И.В.
Дискретный анализ. – СПб.:
центр издательских систем Санкт-Петербургского
Государственного Института Точной Механики и
Оптики, 1998, страницы 50-54, 94-95;
 Итак, с точки зрения
программирования, Жизнь – трудоёмкая, для
компьютера, задача, так как требует довольно
больших ресурсов машины на непрерывный пересчёт
состояний моделируемого мира (под “миром”,
здесь и далее, будет пониматься плоскость,
разбитая на клетки, на которой рассматривается
колония). В чём же этот пересчёт заключается?
Фактически, на каждой итерации нужно разрешать
отношение соседства между конкретными
объектами, то есть, уметь узнавать, сколько у него
соседних клеток. Эта статья и посвящена именно
тому, как это сделать максимально эффективно
(ясно, что вариант полного перебора мест
гипотетической дислокации клеток мы
рассматривать не будем, тем более, что его
применение проблематично на “бесконечных”
полях, которые и представляют основной интерес
при моделировании процесса Жизни). Далее под
“местами” будем понимать позиции, на которых
могут стоять клетки, элементарную область в
рассматриваемом мире (“A” на
рисунке 1), а под “клетками” – места, в которых
есть жизнь (“B” на том же
рисунке).
Итак, с точки зрения
программирования, Жизнь – трудоёмкая, для
компьютера, задача, так как требует довольно
больших ресурсов машины на непрерывный пересчёт
состояний моделируемого мира (под “миром”,
здесь и далее, будет пониматься плоскость,
разбитая на клетки, на которой рассматривается
колония). В чём же этот пересчёт заключается?
Фактически, на каждой итерации нужно разрешать
отношение соседства между конкретными
объектами, то есть, уметь узнавать, сколько у него
соседних клеток. Эта статья и посвящена именно
тому, как это сделать максимально эффективно
(ясно, что вариант полного перебора мест
гипотетической дислокации клеток мы
рассматривать не будем, тем более, что его
применение проблематично на “бесконечных”
полях, которые и представляют основной интерес
при моделировании процесса Жизни). Далее под
“местами” будем понимать позиции, на которых
могут стоять клетки, элементарную область в
рассматриваемом мире (“A” на
рисунке 1), а под “клетками” – места, в которых
есть жизнь (“B” на том же
рисунке).  Будем хранить в
нём информацию о существующих клетках на данный
момент времени. То есть, если место с
координатами x0 и у0 является клеткой, то в массиве
должен присутствовать элемент, имеющий поля со
значениями x0 и y0. Пусть на данном шаге моделирования
у нас будет заполнено n
элементов. Так как размеры популяции, как
правило, не постоянны во времени, то n будет меняться от итерации к
итерации. Вот вам и очевидное ограничение: n не может превосходить m!
Будем хранить в
нём информацию о существующих клетках на данный
момент времени. То есть, если место с
координатами x0 и у0 является клеткой, то в массиве
должен присутствовать элемент, имеющий поля со
значениями x0 и y0. Пусть на данном шаге моделирования
у нас будет заполнено n
элементов. Так как размеры популяции, как
правило, не постоянны во времени, то n будет меняться от итерации к
итерации. Вот вам и очевидное ограничение: n не может превосходить m!


