Автор: Леонид Дурман, durman@inbox.ru
Дата публикации:24.05.2001
Благодарности:
Константину Кнопу, Георгию Башилову и Сергею
Леонову за помощь в подготовке этого материала к
печати
Практически все компьютеры, которые используются людьми, выполняют очень мало полезной работы. Большую часть времени, которое они находятся во включенном состоянии, они только потребляют электричество. На компьютерах набирают тексты, ведут бухгалтерию, бродят по Интернету, играют в игры и т.д. Но ведь потенциал современных компьютеров гораздо выше. Обработка нажатий на клавишу или щелчок мыши занимает микросекунды, а оставшееся время процессор ничем не занят, превращая компьютер в дорогой обогревательный прибор. Можно даже сказать, что обычный PC 99% своей мощности не использует в течении всего срока эксплуатации.
"Компьютерра" не раз рассказывала о распределенных проектах, позволяющих не только обогревать комнату, в которой стоит ваш компьютер, но и делать полезные вычисления параллельно основной работе. Известный проект SETI@Home ищет слабые сигналы от других миров и пытается сделать новые открытия в астрономии. Математический проект GIMPS1 ищет самые большие простые числа Мерсенна которые имеют вид Mp=2p-1 и даже предлагает крупный денежный приз в случае обнаружения нового простого числа Мерсенна. За 5 лет работы этого проекта (при использовании десятков тысяч компьютеров во всем мире) найдено только 4 таких числа.
Но в SETI@Home не ясны реальные результаты отдельного участника, а в GIMPS забрать приз еще менее вероятно, чем выиграть иномарку у Якубовича.
Дорогой читатель, надеюсь, Вы не являетесь Геростратом, который сжег храм Артемиды, чтобы оставить свое имя в истории. Возможно, Вы не Эйлер. Но все же Вы хотите, чтобы Ваше имя осталось в истории навечно? У вас есть хороший шанс - став участником распределенного проекта "Поиск делителей для чисел Ферма" (FermatSearch). Проект создан русским человеком, автором этой статьи. И я попытаюсь подробно рассказать любителям математики и компьютеров об этой затее.
Простые числа будоражили воображение математиков с древнейших времен. Еще Евклид доказал, что простых чисел бесконечно много, но их распределение носит весьма неравномерный характер. Есть простые числа-близнецы, разность между которыми равна 2, но существуют сколь угодно большие промежутки, в которых простых чисел нет. Поэтому распределение простых чисел было названо заколдованным. Были предприняты попытки построить функции, значениями которых были бы только простые числа, но и таких функций пока нет2. Можно доказать, что никакой многочлен, отличный от постоянной, с целыми коэффициентами не может для всех n или для всех достаточно больших n, представлять простые числа. Вполне естественным является рассмотрение показательных функций типа:
f(n)=an ± bn, где a, b, n -целые числа.
Для случая когда берется знак минус:
an - bn=(a-b)(an-1+an-2b+...+bn-1)
в этой формуле простые числа могут появиться лишь при a - b=1 и простом показатели степени. Для a=2, b=1 получаются числа Мерсенна. Во втором случае число:
an + bn=(a+b)(a2n-a2n-1b+...+b2n)
может быть простым лишь тогда, когда n является степенью числа 2. Для a=2, b=1 получаются числа вида:
Fm= ![]()
Первым человеком изучавшим эти числа был величайший математик средневековья Пьер Ферма, позже числа данного вида назвали в его честь. В письме датированное 25-м декабря 1640 года к своему другу и коллеге Мерсенну Ферма заметил, что при m=0, 1, 2, 3, 4 (соответственно F0=3, F1=5, F2=17, F3=257, F4=65537) все эти числа являются простыми. Он считал, что F5=429496729 простое число, так как не смог найти для него делитель. и попытался "догадаться", что все числа этого вида простые. Ни Мерсенн, ни Ферма не решали эту проблему, хотя могли бы. В том же 1640 году Ферма доказал свою малую теорему:
"Для всякого простого числа p и натурального x число xp-1 -1 делится на p".

Если не делится, следовательно p не является простым числом. Используя свою теорему, Ферма мог бы проверить 5-е число, использовав всего 32 операции возведения в квадрат по модулю 232+1, получил бы число 3029026160 и этим доказал, что F5 составное, даже не находя его делителей. Начиная с 1640 г. Ферма упорно искал доказательство для своего ложного предположения относительно простоты чисел Fm и предлагал найти его своим корреспондентам. В 1659 г. Ферма в письме к Каркави уже указывал, что теорема о простоте Fm может быть доказана методом бесконечного спуска. Потребовалось 92 года и гений Леонарда Эйлера, чтобы опровергнуть это утверждение. Эйлер разложил F5 на множители: 641 и 6700417. Ему было тогда 25 лет и он любил разные вычислительные задачи. Но для достижения этого результата он действовал не вслепую (в конце жизни великий Эйлер ослеп на один глаз от титанической вычислительной работы, которую сумел выполнить в рекордно короткий срок), а доказал факт, что всякий делитель числа Ферма имеет вид k*2m+1 +1. Таким образом, Эйлер проверял всего 10 делителей вида 64k+1.



В 1878 Эдуард Люка (Lucas) усилил этот результат: каждый делитель числа Ферма имеет вид: k*2m+2 +1 при любом k.
Когда "королю математиков" Карлу
Гауссу было всего 19 лет, он доказал, что с помощью
циркуля и линейки можно построить правильный N-
угольник для простого N тогда и только тогда,
когда N=Fm=![]() - простое число. Таким образом,
можно построить 3, 5, 17, 257 и 65537 угольники. Сам Гаусс
построил 17 -угольник. Ришело на 80 страницах
указал построение 257 угольника. В гёттингенской
библиотеке в чемоданах больших размеров
хранится способ построения правильного
65537-угольника, выполненное неким Гермесом. По
этому поводу Джеймс Литлвуд пошутил: "Один
навязчивый аспирант достал своего руководителя,
и тот сказал ему: "Идите и разработайте способ
построения правильного 65537-угольника!"
Аспирант ушел и вернулся только через 20 лет".
Как видите, многие величайшие математики
увлекались этими забавными числами. Увлечение
это не пропало и сегодня, особенно с
возникновением компьютеров. А с приходом в нашу
жизнь Интернета усилия людей разных стран стали
совместными.
- простое число. Таким образом,
можно построить 3, 5, 17, 257 и 65537 угольники. Сам Гаусс
построил 17 -угольник. Ришело на 80 страницах
указал построение 257 угольника. В гёттингенской
библиотеке в чемоданах больших размеров
хранится способ построения правильного
65537-угольника, выполненное неким Гермесом. По
этому поводу Джеймс Литлвуд пошутил: "Один
навязчивый аспирант достал своего руководителя,
и тот сказал ему: "Идите и разработайте способ
построения правильного 65537-угольника!"
Аспирант ушел и вернулся только через 20 лет".
Как видите, многие величайшие математики
увлекались этими забавными числами. Увлечение
это не пропало и сегодня, особенно с
возникновением компьютеров. А с приходом в нашу
жизнь Интернета усилия людей разных стран стали
совместными.
На сегодняшний день неизвестно, конечно или бесконечно количество простых чисел Ферма. Существуют весьма сильные аргументы как за одну так и за другую гипотезу.
Чтобы доказать, что число Ферма не простое, существует два принципиальных способа:
1 способ. Найти хотя бы один делитель.
2 способ. Воспользоваться детерминированным
тестом Пепина.
Теорема. Число Fm простое тогда и только
тогда, когда 3(Fm-1)/2+1 делится на Fm
В отличие от чисел Мерсенна, числа Ферма растут невообразимо быстро, грубо говоря, n-e число Ферма это 2n-е число Мерсенна. За прошедшие после Ферма 360 лет человечество не обнаружило больше простых чисел Ферма, но и найти делитель для него весьма не тривиальная задача.
Из за большой редкости делителей и сложности их обнаружения каждый человек, нашедший новый делитель числа Ферма, попадает в историю математики. За три с половиной века поиска известно немногим более 200 делителей. На сегодняшний день -(май 2001 года) список их первооткрывателей включает 60 человек из разных стран мира.
Немецкий профессор Вилфрид Келлер (Wilfrid Keller) ведет сегодня официальную статистику всех известных делителей чисел Ферма: http://www.prothsearch.net/fermat.html. Существует несколько способов обнаружения простого делителя у числа Ферма. Самым простым, распространенным и достаточно эффективным способом является поиск по числам вида k*2n+1 - тривиальное деление.
В 1855 году немецкий астроном Томас Клаусен в письме к Гауссу сообщил о разложении 6-го числа Ферма F6=274177 * 67280421310721, но этот факт оставался более века неизвестным и еще три человека независимо, позже находили этот результат.
Уральский самоучка священник-математик Иван Михеевич Первушин прославился открытием трех чисел. В заявлении датированное 25 сентября 1870 году Первушин сообщает, что число Мерсенна 261 -1 -простое, которое тогда было известно, как самое большое простое число, именно это число стали называть "числом Первушина". В 1877-78 годах он находит два делителя: 114689 делит F12 и 167772161 делит F23

В 1903 году Вестерн (Western) за год титанической работы находит независимо пять новых делителей для различных чисел Ферма и после этого сообщает, что у любого числа Ферма не существует больше делителей меньше миллиона.
В докомпьютерную эпоху работа с этими числами занимала долгие недели и месяцы кропотливых вычислений. И одним из самых внушительных ручных результатов был показан в 1905 году Морхед (Morehead) он нашел простое число 5*275+1 которое делит F73 (число имеющее 2843147923723958851728 знаков, фактически записать которое нет никакой возможности).
Всего же ручным способом за 3 века было найдено лишь 16 делителей для чисел Ферма.
Рафаэль Робинсон (Raphael Robinson) в начале 50-х нашел 20 делителей на одном из первых компьютеров SWAC. Это было одной из первых демонстраций превосходства электронных устройств над ручными вычислениями. Он один из первых показал очень хороший путь отыскания делителей на компьютерах. Для потомков оставил код программы, который в несколько измененном виде использовали многие десятилетия различные искатели. Предварительно он опубликовал таблицу всех простых чисел вида k*2n+1 для n<500 и k<100, а потом среди этих простых чисел отыскал делители чисел Ферма. В дальнейшем эти таблицы расширялись и находились другие делители для чисел Ферма.
На сегодняшний день самым плодовитым искателем делителей для чисел Ферма является американский разработчик компьютерных систем Гари Гостин (Gary Gostin), который на суперкомпьютерах в разные годы нашел уже больше 6-и десятков делителей. В 1993 году он приостановил свои вычисления.
Один из ярых охотников за Ферма числами японец Тадаси Таура (Tadashi Taura) открыл 16 делителей. Он настолько увлечен этим занятием, что собирает самую разнообразную компьютерную технику, часто без HDD и прочих принадлежностей, и объединяет все это в немыслимый вычислительный центр на дому. (Я думаю, его мощность порядка 20-30 гигафлоп. Это уже близко к серьезным вычислительным станциям.)
Многие другие искатели проводят свои собственные вычисления довольно успешно (часто на своих собственных программах), работая в одиночку или переписываясь только с теми, кого знают.

Тест Пепина применялся в том случае, если невозможно было обнаружить обычным делением хотя бы один делитель. В 1905 и 1909 году любитель гигантских вычислений Морхед доказывает этим способом, что F7 и F8, не являются простыми, но ни один делитель ему не был известен. Чтобы судить о проделанной работе например для F8, для этого необходимо 256 раз возводить в квадрат и находить остаток от деления 78-и значного числа. Быстро сегодня, уважаемый читатель, сможет найти остаток от деления ручным способом например двух маленьких чисел 3485653281 и F4=65537 ? А последнее имеет всего 5 знаков.
Максимальное применение теста Пепина было осуществлено в 1999 году. Используя большое количество мощных компьютеров, применяя современный FFT-алгоритм (Fast Fourier Transformer -быстрое преобразование Фурье) для умножения больших чисел и сложнейшие методы оптимизации, вычисление разбили на несколько этапов. После 200 дней работы был получен ответ: "F24 не является простым". Это было одним из самых крупнейших вычислений на компьютере, давшим ответ на простой вопрос: "Да" или "Нет". Это число имеет 5050446 десятичных знаков. Узнать другие технические подробности этого достижения и скачать код можно на http://www.perfsci.com/F24. Профессор Ричард Крендал (Richard Crandall), являвшийся руководителем этих вычислений тогда заявил: "На любой современной технике подобные расчеты для F31 (646456994 знаков) займут как минимум 10000 лет. Это как раз до следующего ледникового периода. Но наряду с ростом мощности компьютеров находятся более совершенные способы проверки. И все же число F31 так велико, что в ближайшие 20 лет мы ничего не сможем определенного сказать о нем, разве что в пределах 100 лет". Сведущие люди шутят, что найти делитель для этого числа сложнее, чем слетать на Луну, если конечно оно не простое.
В 1970 году Моррисон (Morrison) и Бриллхарт (Brillhart)
смогли разложить на множители F7=(116503103764643*29+1)*(11141971095088142685*29+1),
использовав вместо деления последовательный
метод разложения цепной дробью. Десять лет
спустя Ричард Брент (Richard P. Brent) и Джон Поллард (John
M. Pollard) разложили на множители F8,
применив так называемый Rho -метод Полларда.
В 1990 году был получен еще более удивительный
результат. Ленстра (Lenstra), Манасс (Manasse) и большая
группа математиков, используя 700 рабочих станций
Sun в течение нескольких недель с применением метода
решета числового поля, разложили F9,
один из делителей которого имеет вид:
362128936829849024182024971631805407255830459
520272960891514314523640507570656742232821636
569307*211+1
Такой результат, конечно, не может быть получен тривиальным способом вообще никогда.

В 1995 году Ричард Брент сумел разложить F10, применив метод эллиптических кривых (Elliptic curve factoring method - ECM). Один из найденных им множителей F10 имеет аж 252 десятичных знака. Ричард Брент весьма известный и плодовитый математик сегодняшнего дня, для всех, кто интересуется математикой и желающих поглубже познакомиться с передовыми темами в Теории чисел, криптографии, алгоритмах и многими другими темами, очень советую посмотреть его персональный сайт, там вы можете найти такой объем исчерпывающей информации и документации по этим темам, которой вы не встретите больше нигде.
На сегодняшний день мы знаем судьбу всех чисел Ферма до F32 включительно. Для большинства из этих чисел известны также их делители, кроме m=14, 20, 22, 24. Для разложения больших чисел наилучшим сегодня является ECM, тесно связанный со стойкой криптографией и находящийся на переднем крае математической науки.
Вы также можете принять участие в обнаружение подобных новых делителей для малых чисел Ферма m < 24 и даже побороться за денежные призы. Но начиная с n=25, ECM- алгоритм и другие алгоритмы становиться использовать весьма проблематично, так как ему необходимо иметь дело со многими миллионами знаков.
| Годы | Интервал в годах | Найдено делителей |
|---|---|---|
| 1640-1731 | 92 | 0 |
| 1732-1854 | 123 | 2 |
| 1855-1900 | 46 | 7 |
| 1901-1952 | 52 | 7 |
| ВСЕГО | 313 | 16 |
| Годы | N | Годы | N | Годы | N | Годы | N | Годы | N | Годы | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1961 | - | 1971 | - | 1981 | 3 | 1991 | 12 | 2001 май | 10 | ||
| 1962 | 2 | 1972 | - | 1982 | 2 | 1992 | 10 | ||||
| 1953 | 2 | 1963 | 11 | 1973 | - | 1983 | 2 | 1993 | 10 | ||
| 1954 | - | 1964 | - | 1974 | 2 | 1984 | 7 | 1994 | 1 | ||
| 1955 | - | 1965 | - | 1975 | - | 1985 | 2 | 1995 | 8 | ||
| 1956 | 14 | 1966 | - | 1976 | 2 | 1986 | 12 | 1996 | 7 | ||
| 1957 | 6 | 1967 | - | 1977 | 4 | 1987 | 5 | 1997 | 4 | ||
| 1958 | - | 1968 | - | 1978 | 2 | 1988 | 4 | 1998 | 8 | ||
| 1959 | - | 1969 | - | 1979 | 13 | 1989 | - | 1999 | 9 | ||
| 1960 | - | 1970 | 2 | 1980 | 9 | 1990 | 8 | 2000 | 13 | ||
| 22 | 15 | 32 | 45 | 82 | 10 |
Если взглянуть на логарифмическую диаграмму
распределения делителей чисел Ферма, то можно
заметить, что они расположены весьма равномерно.
Другими словами, чтобы находить новые делители,
необходимо каждый раз затрачивать
экспоненциальные усилия. Так что сила любого
"железа" - это карлик перед Гигантом.
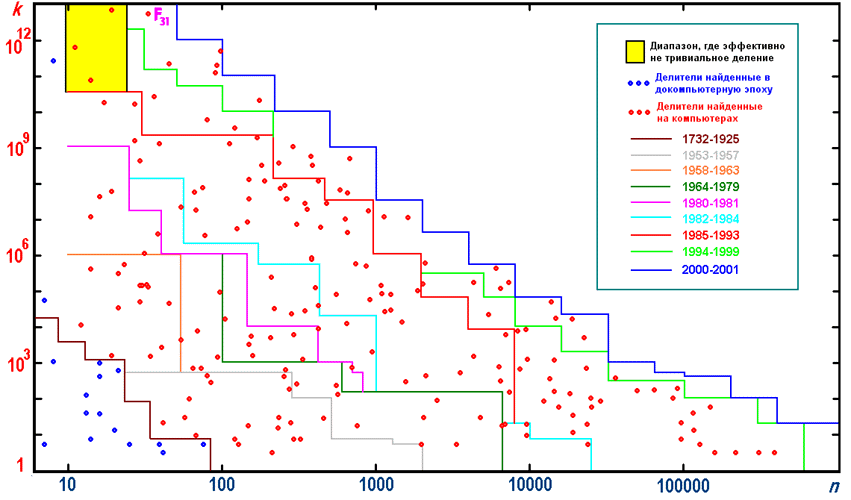
До 1997 года не было каких-либо объединенных усилий по поиску больших "не Мерсенна" чисел. Но француз Ив Галло (Yves Gallot) написал отличную программу Proth.exe, которая может находить огромные простые числа многих видов, причем на самых обычных PC. После этого последовал буквально взрыв в этой области исследований. Его программа стала лучшей и весьма популярной. Она может гоняться за очень большими простыми числами, а в основе его программы лежит FFT-алгоритм. Большинство рекордных простых чисел, найденные (на суперкомпьютерах) до появления этой программы, сегодня не входят даже в сотню3. Программа Галло, в частности, может находить и делители для чисел Ферма. За 3 года поиска его программой найдено еще 11 новых делителей для очень больших чисел Ферма. На сайте http://www.prothsearch.net/ можно найти программу и инструкции о том, как принять участие в проекте Proth по поиску гигантских простых чисел.
В начале 2000 года, просматривая страничку Келлера, я заметил, что ECM-проект охватывает малые числа. Поиск при помощи Proth забрался высоко в небо. А кто же сегодня работает над средними числами Ферма? Я знал только о японце Тауре, который бороздит это пространство, собирая неплохой урожай. Но свою программу он не публикует, а программа Галло эффективна только для больших чисел. Тогда я взял в руки карандаш и прикинул возможности. Бог мой! Да ведь шустрая программка на ассемблере для современных процессоров сможет реально поднять планку и обнаружить делитель. Первая рабочая версия программы была готова в апреле. Я назвал ее "Fermat" в честь основателя этих чисел.
По умолчанию программа работает при самом низком приоритете, давая возможность забирать ресурсы любой другой программе когда и сколько ей захочется. Она использует только свободные и неиспользуемые циклы процессора, то есть не препятствует работе других программ в системе. В принципе она мирно уживается даже с "хранителями экрана", лишь немного медленнее выполняя свою работу. Я старался делать массив, используемый в программе для вычислений, как можно компактнее, не выходя за рамки второго кэш, а код оптимизируя под современные процессоры. И тесты показали, что на Celeron и PIII программа практически одинаково бежит на той же частоте, что редко можно встретить у программ-монстров.
Довольно быстро был найден первый делитель, чему я был весьма рад, но нисколько не удивился, так как программа имела хороший "запас прочности". Совершенствуя свою программу, к осени 2000 я нашел уже 3 новых делителя (все - на скромных Celeron'ах), а Келлер сообщил, что я попал в зарубежные публикации. Но как я уже сказал, чтобы делать дальнейшие шаги, нужны новые огромнейшие усилия. Самое главное - что никто в мире не знал, кто и где работает, а страничка Келлера не давала ответ на этот вопрос, то есть многие люди дублировали одну и туже работу.
Неожиданно стали поступать письма с просьбой дать программку для исследования "16-й догадки Риверы"4 и для поиска делителя F31. Это было последней каплей в моих сомнениях.
В Интернете не было единого проекта по исследованию чисел Ферма - вторых по знаменитости чисел. Мои знания английского более чем скромны, но это не стало препятствием. Используя автоматизированные переводчики, я поместил в Интернете программу и информацию о проделанной работе. Так мы встретились с коллегами, и каждый участник проекта сообщил, где он работает. Моя поначалу одинокая Web-страничка начала обрастать информацией, а программа Fermat заняла свободную нишу как самая быстрая программа для средних чисел Ферма.
Первыми участниками проекта стали почти все, работавшие до той поры раздельно искатели, а так же системные администраторы и программисты. На сегодняшний день охвачены представители всех континентов, кроме Антарктиды и Африки. Вероятно, у первых компьютеры еще не нагрелись, а у вторых уже перегрелись5.
В конце 2000 года на авансцену возвратился главный "пожиратель" чисел Ферма Гари Гостин вместе с тремя суперкомпьютерами от Хьюлетт-Паккард. И пока на сегодня он в десять раз превосходит по компьютерной мощи всех остальных участников, вместе взятых. Но, надеюсь, это дело времени.
Последние лет 10 новый делитель обнаруживается в среднем раз в полтора-два месяца, но в конце декабря 2000 года последовал взрыв - пять дней подряд каждый день отыскивался новый делитель! Этим залпом было отмечено новое тысячелетие. Три из пяти этих делителей были найдены на домашних компьютерах. Хорошие темпы, можно даже сказать рекордные темпы обнаружения делителей сохраняются и сегодня, причем обычные ПК опережают в этом плане суперкомпьютеры.
Наш проект свободный, то есть каждый участник может использовать любую программу, скачав ее с сайта или написав самостоятельно, но наиболее важной является динамическая информация, какие диапазоны свободны для дальнейшего вычисления. В планы входит создание полностью автоматического сервера наподобие популярного GIMPS: вы выходите в Интернет, а программа узнает об этом и отсылает на сервер информацию о проделанной работе и, если вычисления закончились, берет новую задачу. В начале этого года реальную помощь в проекте предложил итальянец Луиджи Морелли (Luigi Morelli), один из главных системных администраторов в Италии. Он предоставил нормальный сервер, домен и включился в создание этой самой автоматической базы данных.
Мы не можем доказать простоту большого числа Ферма, но мы можем постоянно исключать из списка все больше и больше заведомо не простых чисел Ферма, находя делители и накапливая статистику для будущих открытий в математике. Как известно, очень многие законы были обнаружены благодаря своевременно подмеченным закономерностям.
Сегодня единственный известный способ поиска для m>25 - это тривиальный перебор простых делителей, имеющих вид:
D=k*2n+1, где n>m+2.
Операция деления Fm на D относительно простая, так как в ней используется модулярная арифметика. Чтобы доказать, что Fm делится на D, необходимо произвести m раз вычисления по рекуррентной формуле:
Si=S2i-1 mod D (1)
где S0=2. Если Sm= -1 то делитель найден. Кроме того, можно ускорить вычисления в разы, если не искать делитель для конкретного Fm, а, взяв фиксированное n и нечетное k, выполнять вышеуказанные действия не более n-2 раз, проверяя каждый раз условие Si= -1. Другими словами, поиск делается так: может ли фиксированный делитель делить какое-нибудь число Ферма? 6.
На первый взгляд кажется лишь одна маленькая простая формула, но не так все просто. При этих вычислениях приходится сталкиваться с числами превышающими разрядность компьютеров, а при более внимательном рассмотрении приходится решать ряд не тривиальных задач. В известной Библии для программистов Дональд Кнут 7 собрал численные алгоритмы почти на все случаи жизни, в том числе и для решения этих проблем. Примем
S2=X*2n+Y (2)
где числа X иY получаются отсечением n бит в двоичном представлении числа S2. Если k менее разрядности компьютера, то мы может относительно легко вычислить два числа q -частное и r -остаток полученные при делении X на k. Тогда выражение (2) можно записать:
S2=Y-q+2nr (mod k. 2n+1)
Но самой длинной и сложной операцией является возведение в квадрат. Если это делать "классическим" методом, то его сложность пропорциональна n2. Для больших чисел (больше тысячи знаков) это становится серьезной проблемой. Но математики нашли выход. В 1968 году Ф.Штрассен (V.Strassen) применил дискретное преобразование Фурье для умножения больших чисел. В этом случае необходимое количество вычислений пропорционально n*ln(n). Благодаря этому сильному методу стали реальными многие другие вычисления, используемые для практических целей. В частности, биологи используют его при расшифровки генома человека, а компьютерщики - при сжатии звука и видео. Математические работы в этой области продолжаются и по сей день. Это очень большая и серьезная тема, которая не может быть рассмотрена в такой маленькой статье. Интересующиеся могут зайти на специальный сайт посвященный этим работам http://www.fftw.org/
Как бы там ни было, процесс модулярного деления Fm на D требует больших затрат времени. Чтобы ускорить процесс перебора, мы должны брать "подходящие" делители. Подходящим может быть только число D, если оно простое (если D не простое, мы его отбрасываем). Наша задача несколько упростилась. Но для дальнейшего повышения эффективности вычислений необходимо еще и быстро устранять большинство D.
Достаточно в начале всех вычислений найти много простых чисел p, тогда для каждого p находим такое k0, чтобы соблюдалось тождество
k0*2n= -1 (mod p)
Очень простое решение недавно показал Паул Джоблинг (Paul Jobling) получая после преобразования:
-k0=((p+1)/2)n(mod p)
Тогда мы сможем применить известное со школы решето Эратосфена и просеять все неподходящие k, как k0, k0+p, k0+2p... Если взять 100000 простых чисел, то отбрасывается примерно 92% нечетных k.
Еще один прием оптимизации любой численной программы состоит в использовании умножения на обратную величину вместо операции деления. То есть один раз вычисляем значение 1/x, а затем используем только операцию умножения. С неточным результатом при округлении 1/x можно бороться, есть способы. Операция деления самое слабое место любого процессора выполняется за 38-40 тактов. Для операции умножения необходимо менее 4 тактов на любом современном процессоре. Посмотрите внимательно: основная наша задача - это делить числа, но во всем основном алгоритме программы Fermat нет ни одной команды деления.
Я до сих пор не могу в это поверить. 12 апреля 2001 года, в день полета в космос Юрия Гагарина, произошло важное событие. Немец Александр Круппа (Alexander Kruppa) используя программу MFAC Тони Форбеса (Tony Forbes) обнаружил долгожданный делитель для особенного числа у математиков F31 Вот этот делитель 5463561471303*233+1=46931635677864055013377. В этот день все интересующееся математическое общество буквально всколыхнулось, все друг друга поздравляли и отмечали этот удивительный факт. Ричард Кренделл тут же отметил, что этот делитель не мог быть обнаружен другими эффективными методами, например методами "p-1"и "p+1". По редкости этот факт сравним с полетом на Луну.
Почему число F31=22147483648+1 особенное? Дело в том, что это было последнее число Ферма, на которое математики возлагали надежду, что оно окажется простым и которое теоретически могло быть проверено хотя бы в ближайшие лет сто на будущих суперкомпьютерах. Если бы оно оказалось простым, тогда был бы абсолютно побит рекорд самого большого известного простого числа, против которого сегодняшний рекорд, число Мерсенна: 26972593-1, оказался бы ничтожно мал. Видимо, все же придется переосмыслить гипотезу о бесконечности простых чисел Ферма. Следующее число Ферма, характер которого не известен, - F33. Если не удастся обнаружить для него относительно небольшой делитель, то доказать его простоту наверное человечество не сможет никогда. Начинается новая дьявольская гонка по устранению этих и других чисел из списка теоретически претендующих на самое большое известное простое число.
На момент написания этой статьи из 60 человек исторического списка только трое россиян. Почему так мало? Неужели русская школа программирования столь слаба или у нас хуже компьютеры?
Мы сейчас в самом начале пути. Прикиньте свои возможности. Вы не знаете чем бы занять свой компьютер, кроме игрушек? Или Вы опытный программист, который хочет испытать свои способности? Вы просто любитель математики и компьютеров? Если хоть раз вы кивнули, милости прошу, присоединяйтесь. Еще очень многое надо сделать. Подробности, как говорится, на сайте проекта FermatSearch.org.
P.S. Когда статья была уже готова, еще один шаг сделал германский профессор Петер Гробстиш (Peter Grobstich), он нашел делитель: F94 разделился на 482524552001*297 + 1 используя программу Fermat.exe. Гробстиш так горд этим открытием, что сразу же создал сайт о своей работе и своем открытии.
Кто следующий?
Все известные делители можно найти здесь http://www.prothsearch.net/fermat.html.
Обсчитываемые сегодня диапазоны можно увидеть
здесь http://www.fermatsearch.org/status.htm
Историческую таблицу всех людей и подробности по
ним можно найти здесь http://www.fermatsearch.org/history.htm
| 1) "Компьютерра" №358, 359. Адрес SETI@Home: http://setiathome.ssl.berkeley.edu/ "Компьютерра", №211 (1997 г.). Адрес проекта GIMPS - http://www.mersenne.org/ |
|
| 2) В Интернет существует распределенный проект, который занимается вычислением реальных значений функции pi(x) - количества простых чисел, не превосходящих x. Можно посмотреть на красивые диаграммы и поучаствовать: | |
| 3) Профессор Крис Колдуэлл (Chris K. Caldwell) ведет список из 5000 самых больших простых чисел всевозможных видов: http://www.utm.edu/research/primes/largest.html | |
| 4) Крэйг Джонсон (Craig Johnston) высказал предположение, что не существует простых чисел формы S(n)=nn +1, для n>4, Вацлав Серпинский доказал (1958), что S(n) простое только тогда, когда простое число Ферма: Fm, m=j+2j и n=2^(2j), для j>0 http://www.computerra.ru/online/firstpage/knopki/9728/www.primepuzzles.net/conjectures/conj_016.htm, то есть достаточно доказать не простоту соответствующего числа Ферма. | |
| 5) В Бразилии температура воздуха в офисах частенько держится в районе 380 С и, как сообщал мне знакомый тамошний сисадмин, у них процессоры довольно часто сгорают, там вообще не занимаются разгоном. В Африке обстановка еще тяжелее. | |
| 6) До сих пор в Интернете публикует свои работы некий Joe McLean's, который проделал гигантский объем работ в поисках делителя для конкретного числа Ферма, но ему не суждено было найти новый делитель таким путем, хотя мог бы добиться успеха на имеющихся вычислительных ресурсах. | |
| 7) Дональд Э.Кнут "Искусство программирования" тт.1-3. ИД "Вильямс", 2000. Рекомендую приобрести эту книгу всем программистам, которые себя таковыми считают. О Д.Кнуте и его работе см. недавнюю тему номера в "Компьютерре" №387. |
Закончено 21 мая 2001