Морской бой

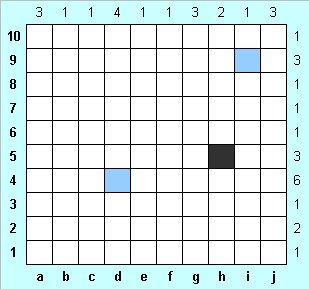На рисунке слева изображено условие задачи. Для удобства строки занумерованы снизу вверх от 1 до 10, а столбцы - слева направо от a до j. Черный квадрат - корабль, или часть корабля, синий - вода. Будем и в дальнейшем обозначать черным цветом части кораблей, а синим - воду. Те места головоломки, которые мы исследуем на текущем ходу, выделяются оттенками этих цветов: корабли изображаем темно-синим цветом, а воду - голубой.

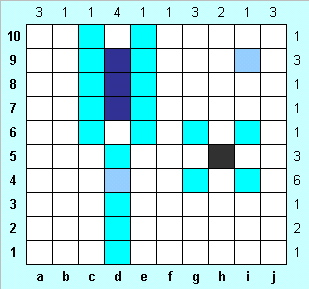Вначале нам пригодится очень простое утверждение: если клетка занята кораблем, то клетка, касающаяся ее углом, обязательно пуста. Отмечаем голубым клетки, соседние с h5. Далее надо попытаться ответить на вопрос, где может находиться четырехпалубный корабль. Поскольку в строке 4 ему нет места, а большинство определяющих чисел меньше четырех, единственное его возможной положение - в столбце d, выше d4. Прикинув самое нижнее и самое верхнее возможное положе ние корабля, рисуем темно-синим те клетки, которые он заполнит в любом случае. Самое нижнее возможное положение (до d5 включительно) невозможно, так как в этом случае клетки с4 и е4 должны быть водой, и в строке 4 окажется пять клеток воды. Отмечаем водой места вокруг четырехпалубного корабля (c6-c10, e6-e10), а также клетки d1, d2, d3.

Отмечаем воду в строках 8 и 7 во всех клетках, кроме занятых кораблем. Поскольку очевидного продолжения не видно, полезно некоторые данные задачи рассмотреть более детально. В первую очередь обратим внимание на большие числа, так как они подразумевают более плотное расположение кораблей. Цифра 6 в строке 4 нам может дать еще некоторую информацию. Поскольку три клетки с водой в этой строке уже известны, то лишь одну клетку с водой можно отметить в ней. Посмотрим, где в строке 5 могут находиться части кораблей. В b5 корабль находиться не может, так как тогда клетки а4 и с4 заполнены водой. Аналогично, если корабль в е5, то и в е4, и в f4 - вода (поскольку в столбце е может находиться лишь один элемент корабля). То же самое можно сказать и про клетку f5, и про с5.

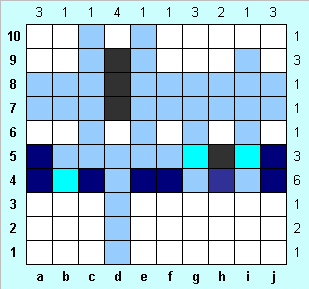Допустим, что части корабля нет в h4. Тогда корабли должны быть в клетках a4-c4, e4-f4 и j4. Получается, что в строке 5 в этом случае никак нет трех фрагментов кораблей. Поэтому отмечаем темно-синим h4, и сразу же голубым - g5 и i5. Теперь все клетки с водой в строке 5 известны, рисуем в остальных клетках этой строки фрагменты кораблей. Так как в b4 - вода, заполняем фрагментами кораблей и строку 4.

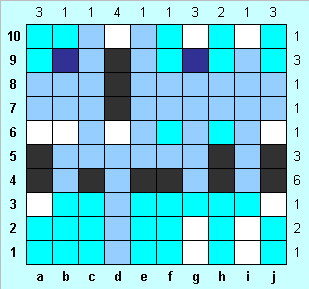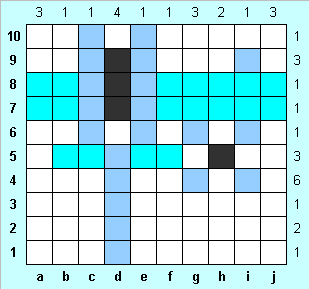
Заполняем голубым клетки b3-i3, а также столбцы с, f , e и h. Убеждаемся, что трехпалубные корабли могут находиться только в столбцах a и j, причем по две клетки каждого корабля нам уже известны. Заполняем голубым те клетки столбцов a и j, в которых трехпалубный корабль находиться не может. Отмечаем в единственно возможных местах строки 9 фрагменты кораблей (в клетках b9 и g9), и голубым - оставшиеся клетки столбца b.

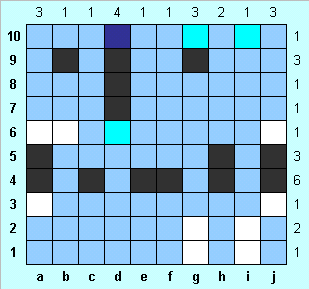Замечаем, что один из трехпалубных кораблей расположен в строках 3-5, а другой - в строках 4-6 (но какой где, пока неизвестно). В любом случае в строке 6 единственная клетка занята трехпалубным кораблем, и d6 - клетка с водой. Четырехпалубный корабль занимает клетку d10, остальные ранее незакрашенные клетки заполняем голубым.

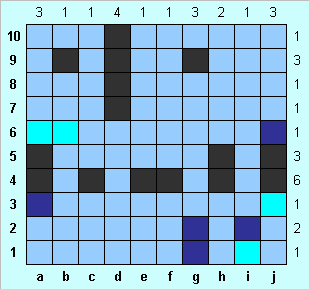Обозначаем двупалубный корабль в клетках g1-g2, воду в i1 и корабль в i2, воду в j1, достраиваем трехпалубные корабли. Убеждаемся, что комплект кораблей получился именно таким, как нужно, что ни один корабль не касается другого. Наконец, проверяем полное соответствие между определяющими числами и количеством клеток, занятых кораблями. Задача решена.

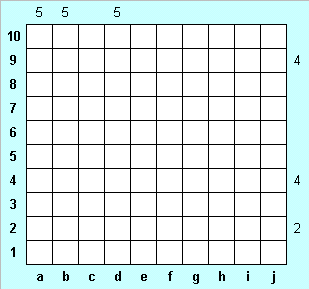Эта головоломка, предлагавшаяся на 5-м Чемпионате мира по пазлспорту, содержит очень мало данных, и, на превый взгляд, не дает никаких зацепок для решения. Но на помощь приходит простое правило: если в клетке корабль, то в клетке, которая касается ее углом, корабля нет. Оно дает очень важное следствие: количество клеток, занятых кораблями, в двух соседних столбцах не более 10. Совсем несложно убедиться, что единственное возможное расположение клеток с кораблями в столбцах а и b - это по паре в некоторых пяти строках. Использование этой ключевой идеи делает дальнейшее решение доступным даже начинающему головоломщику.

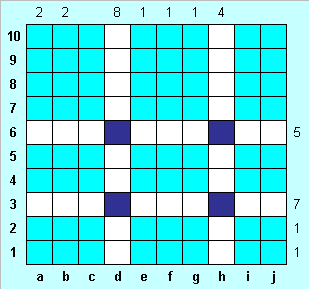В этом примере даже наличие максимально возможной в морском бое цифры 8 не дает возможность существенно продвинуться в решении. Помогает вот какое рассуждение: В столбцах d и h и в строках 3 и 6 общая сумма определяющих чисел - 24. А общее количество клеток, занятое кораблями - 20. Это возможно лишь в случае, если все корабли расположены на вышеуказанных четырех линиях, и клетки на пересечени двух столбцов и двух строк - части кораблей, то есть учитывались дважды. Оставшаяся часть решения уже совсем проста.